8-3 Microscopic Observation of Deformation Process in Metallic Materials

－Computer Modeling of Defect Structure via Atomistic Simulation Methods－

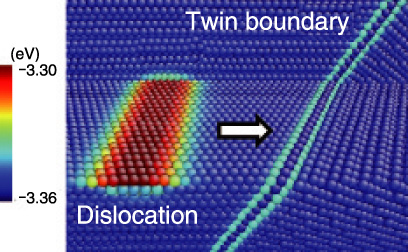
Fig.8-8　Atomic model of defect structures (dislocation and twin boundary)

Fig.8-8　Atomic model of defect structures (dislocation and twin boundary)

An atomic model including a pure edge dislocation and a twin boundary is constructed. Atoms are color-coded according to potential energy.

 

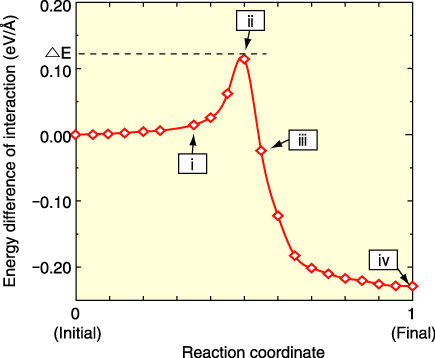
Fig.8-9　Reaction energy of the interaction between dislocation and twin boundary

Fig.8-9　Reaction energy of the interaction between dislocation and twin boundary

The reaction energy along the minimum energy path of the interaction process per unit length of a dislocation is shown. The energy curve has a high energy peak.

 

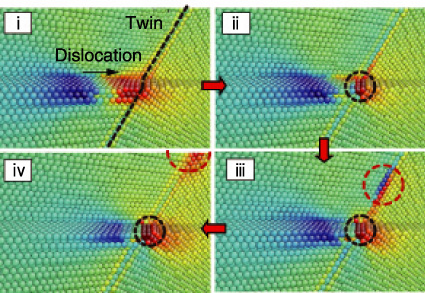
Fig.8-10　Atomic configurations of the defect motion during the interaction process

Fig.8-10　Atomic configurations of the defect motion during the interaction process

Defect motion in the reaction process corresponding to the Roman numerals in Fig.8-9 is shown. The high energy state (ii) is equivalent to the moment of the interaction. Dissociated mobile and immobile dislocations are marked by red circles and black circles, respectively.

Reactor structural materials are constructed mainly from metallic materials. Most metallic materials have a defect structure in which local atomic arrangement is disordered, and mechanical properties such as plastic deformation and crack nucleation are determined by such a defect structure. Additionally, defect structures change from moment to moment under deformation. Therefore, it is important to understand the details of structural changes from the microscopic point of view. Among the various kinds of defect structures, dislocations and grain boundaries are the most significant factors in deformation characteristics and material strength. With the former, there is a disconnect region between planes in crystalline materials, and the latter are defined by the interface between two crystal grains. We investigated structural changes in these two typical defects via computational modeling. An atomic model of a dislocation and twin boundary in aluminum is shown in Fig.8-8. When shear stress is applied to the model, the dislocation is first activated and interacts with the twin boundary. An atomistic transition states method based on a nudged elastic band method was employed to evaluate the interaction process between the dislocation and the twin boundary. The energy difference along the minimum energy path of the interaction process is shown in Fig.8-9. It was found that this process needs to overcome a high energy barrier at the moment of the interaction. Atomic configurations during the interaction are shown in Fig.8-10, where the Roman numerals corresponds to those in Fig.8-9. The highest energy state occurs at the moment when the dislocation is approaching the twin boundary. We described the dissociation of a lattice dislocation into mobile and immobile dislocations. In summary, it was found that the twin boundary acts as a high energy barrier for the dislocation motion and that the dissociation of the glide dislocation gives rise to grain boundary sliding. Thus, we consider that computational simulations demonstrate great potential to understand defect dynamics under deformation at a microscopic level of view.

Reference
Tsuru, T. et al., Fundamental Interaction Process between Pure Edge Dislocation and Energetically Stable Grain Boundary, Physical Review B, vol.79, issue 1, 2009, p.012104-1－012104-4.

 |