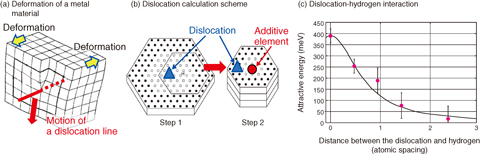
Fig.10-2 Calculation of dislocation and impurity elements
, is introduced to the crystal. The crystal is cut by this plane and atoms located on it are displaced by one atomic spacing. If moves downward, the displacement propagates in the crystal and the crystal deforms.
is conducted, and then, an additive element (
) is introduced and calculation is performed only for the atoms near the additive element. 
and 
denote the atoms for which QM calculations have been performed and omitted, respectively.Owing to their strength and availability, steels are used for various applications in our civilization, such as automobiles, bridges, and nuclear reactors. Modern steels generally contain more than ten separate elements, and their content rates are optimized for specific purposes based on the results of numerous experiments. For example, it has been found that chromium increases corrosion-resistance and phosphorus degrades the steel. Recently, much attention has been devoted to computational materials design, which considers the effect of various elements based on the simulations and big data analysis, for the accelerated development of new materials.
To predict the effect of various elements on the strength of steels, quantum mechanical (QM) calculations are required. The difference in the number of electrons in different elements greatly changes the behavior of electrons in the material and affects various material properties. Calculation of these effects must account for many electrons. The computational time is proportional to the cube of the number of atoms. Even for current supercomputers, several hundred atoms is the maximum possible scale of calculation. Within this limitation, using ingenious calculation techniques, various material properties have been clarified by QM calculations, such as the effect of additive elements on the force required to break the material. However, owing to the complexity of the process, there have been no QM calculations of the deformation properties of metal materials, which is one of their most important properties. Fig.10-2(a) depicts the deformation process of metal materials. A movement of a dislocation line in a material induces a slip on the atomic plane and the material deforms while the crystal structure remains intact. Since the dislocation line is relatively a large-scale structure, calculation of a dislocation line and additive element requires about one thousand atoms, which is impossible.
To solve this problem, we have invented a multi-scale approach wherein QM calculation of a dislocation line is performed first and then an additive element is included in the calculation. QM calculations are performed only for the atoms close to the additive element. By this method, the number of atoms in the QM calculation is reduced to one-third of the original case, allowing the calculation to be treated by current supercomputers. We have applied this method to investigate the effect of hydrogen atoms on the motion of dislocations in iron and found that there is a strong attraction between the hydrogen atom and dislocation, which prevents deformation of iron at low temperature. We will apply this method to various additive elements used in nuclear reactor materials and accelerate the development of improved nuclear materials.
<Previous: 10 Computational Science and E-Systems Research | Next: 10-2 >
(166KB)
