3-5　Exploring the Mystery of Neutrino Masses with Nuclear Physics

－High-Precision Calculation of ββ Decay using the K Supercomputer－

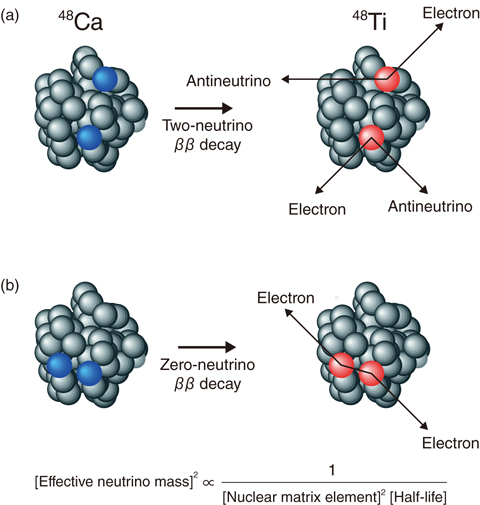
Fig.3-12 Schematic illustration of ββ decay from 48Ca to 48Ti

Fig.3-12 Schematic illustration of ββ decay from 48Ca to 48Ti

(a) Two-neutrino ββ decay and (b) zero-neutrino ββ decay are shown, both of which involve two protons (blue) changing into two neutrons (red). (a) Two neutrinos and (b) no neutrinos are emitted in addition to two electrons in common. (b) In the zero-neutrino ββ decay, the effective neutrino mass, i.e., a particular combination of the masses of three types of neutrinos, is related to the nuclear matrix element and the half-life by the equation displayed.

 

Neutrinos are a type of elementary particle. While the basic properties of neutrinos are indispensable for determining the theory of everything, most of them are still unknown. It has recently been established, on the basis of observations with Super-Kamiokande, that neutrinos are massive particles; however, their absolute masses have not been measured yet. In the present study, we provide reliable nuclear-structure data that are needed to determine neutrino masses from ββ decay by performing large-scale numerical calculations based on state-of-the-art nuclear theory.

ββ decay is a sort of nuclear decay in which two neutrons in a nucleus simultaneously change into two protons, as illustrated in Fig.3-12. This decay has been observed for ∼10 nuclides, including 48Ca, and all the observed decay modes so far are so-called two-neutrino ββ decays, which emit two antineutrinos. It is nevertheless possible to detect another decay mode that does not emit any neutrinos (and is thus called zero-neutrino ββ decay) if neutrinos are their own antiparticles. When the half-life of zero-neutrino ββ decay is measured, neutrino masses can be determined using the equation shown in Fig.3-12(b). In order to derive neutrino masses in this way, however, one has to know how large the nuclear matrix element of zero-neutrino ββ decay is.

The nuclear matrix element is a value that characterizes how easily two neutrons are converted into two protons within a nucleus, depending on proton and neutron numbers. The value cannot be directly determined by nuclear experiment, and therefore, the only way to provide its quantity is calculation based on nuclear many-body theory. Before this study, the nuclear matrix element of 48Ca was estimated through a rather approximate calculation that took only eight nucleons as being active out of 48 nucleons in total. This restriction was owing to the computational limits on treating many nucleons. In the present study, we are successful in conducting a high-precision, large-scale quantum many-body calculation that assumes 32 active nucleons using the K supercomputer. The resulting nuclear matrix element in 48Ca becomes about 30% larger than that of the previous calculation. Since the present calculation considers the leading correction to the previous one, the obtained values should be quite reliable.

At present, zero-neutrino ββ decay is being sought worldwide. If this decay is observed in 48Ca in the near future, we expect that our value will be used to derive neutrino masses.

Reference
Iwata, Y., Utsuno, Y. et al., Large-Scale Shell-Model Analysis of the Neutrinoless ββ Decay of 48Ca, Physical Review Letters, vol.116, issue 11, 2016, p.112502-1-112502-6.

 |