9-1　Acceleration-Flow Analysis in a Nuclear Reactor

－Development of Massively Parallel Communication-Avoiding Matrix Solvers－

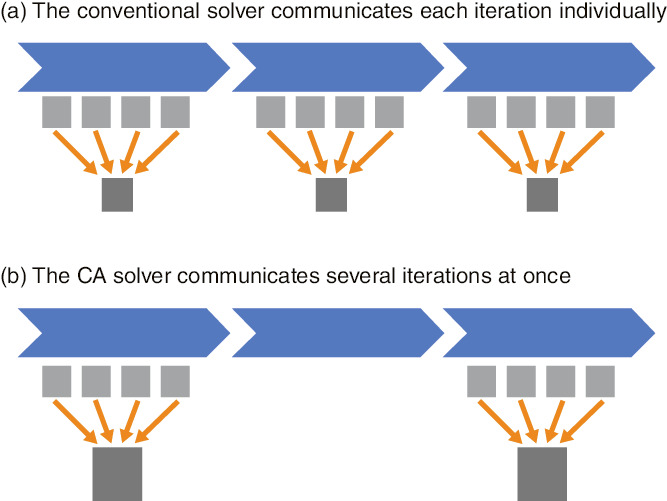
Fig.9-2 Representations of calculation and communication by the conventional and CA solvers

Fig.9-2 Representations of calculation and communication by the conventional and CA solvers

(a) shows the conventional solver, which needs communications indicated by arrows between the processors for each iteration. (b) shows the CA solver, which can communicate data from several iterations at once and reduce communications.

 

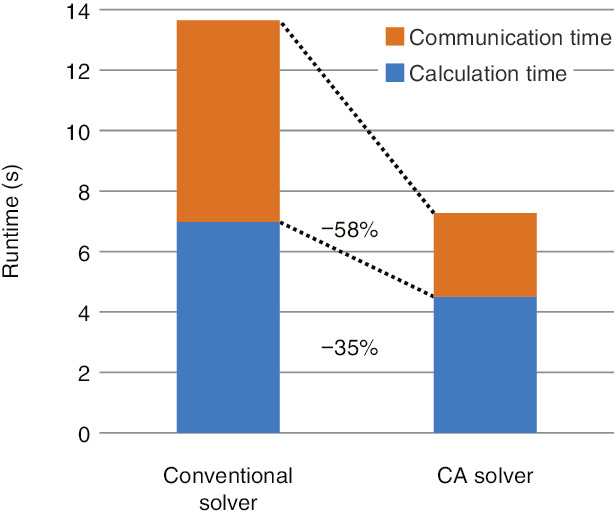
Fig.9-3 Parallel-performance comparison of the conventional and CA solvers

Fig.9-3 Parallel-performance comparison of the conventional and CA solvers

This figure shows the runtime of matrix calculation of the Poisson equation (800 × 500 × 3540 lattice) on the K computer with 30000 nodes. With the CA solver, the communication time, which occupied about half of the whole time of the conventional solver, is greatly reduced and the performance is roughly doubled.

 

We promote the development of a multiphase thermal-hydraulic computational fluid dynamics (CFD) code for analyzing the relocation of molten materials in nuclear reactors during severe accidents. Current supercomputers can simulate the melt-relocation behavior of several fuel assemblies. However, to analyze a severe accident for the whole reactor-pressure vessel, we need exa-scale computers that can perform calculations more than 100 times faster than current supercomputers.

Current supercomputers are based on distributed-memory parallelism with tens of thousands of computers connected by a network. In order to make full use of the supercomputers’ performance, it is necessary to communicate the calculated data and synchronize the steps of processing; however, the communication cost is a bottleneck in exa-scale computers. In multiphase CFD code, the matrix solver for the pressure equation accounts for most of the computational cost. Since the communicational cost of the conventional solver is relatively large, the communication bottleneck becomes obvious in large-scale parallel computation. We developed the communication-avoiding (CA) matrix solver to resolve this issue and further enable large-scale CFD code analysis.

The conventional matrix solver uses the conjugate-gradient (CG) method, an iterative technique. The CG method solves a large-scale matrix problem by calculating the residual of the approximate solution and modifying the solution. The conventional solver requires inner-product operations with global communications, which collect data calculated by tens of thousands of computers per iteration (Fig.9-2(a)).

However, by communicating the data required for inner-product calculation only once for several iterations by changing the algorithm that is mathematically equivalent to the conventional solver, the CA solver can reduce the number of collective communications and synchronizations to a fraction of that of the conventional solver (Fig.9-2(b)). Despite this algorithm change causing the computational cost to become larger, the CA algorithm is suitable because the communication cost is significantly higher than the computational cost in massively parallel processing. We evaluated our CA solver’s performance on the K computer, which is the representative supercomputer in Japan. Because of the tens of thousands of computers involved in massively parallel processing, the communication cost manifested in the conventional solver was greatly reduced. In addition, the changed algorithm decreased the number of memory accesses, accelerating the calculation time and doubling the total performance (Fig.9-3).

We will develop the CA solver for a general matrix library and provide it to the community. The present study was sponsored by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, Post-K Priority Issue 6, “Accelerated Development of Innovative Clean Energy Systems”.

Reference
Mayumi, A. et al., Left-Preconditioned Communication-Avoiding Conjugate Gradient Methods for Multiphase CFD Simulations on the K Computer, Proceedings of 7th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2016), Salt Lake City, Utah, USA, 2016, p.17-24.

 |