The nucleus which has an atomic number of 114 and a neutron number of 184 is called a superheavy element and its existence has been theoretically predicted. Many efforts have been made to synthesize superheavy elements by using accelerators, but they have not yet succeeded. Until now heavy elements up to atomic number 112 have been synthesized with an extremely low production rate, which was technically the limit.
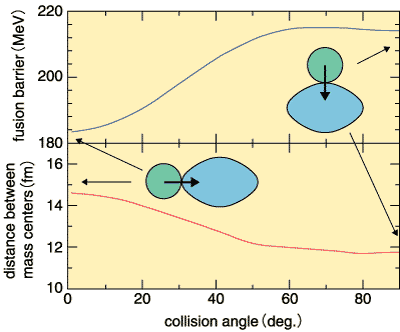
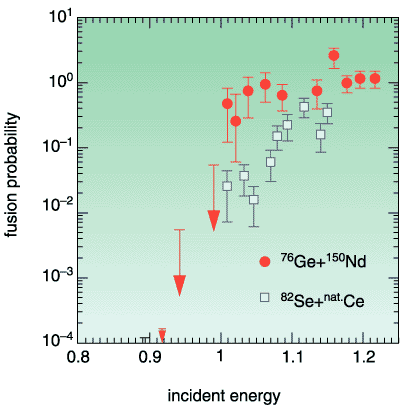
In order to overcome this difficulty, we started to research a new fusion process using a deformed nucleus. Figure 1-3 shows the calculated fusion barrier and the distance between mass centers in the collision with a projectile 76Ge and a largely deformed 150Nd target. The fusion barrier is the lowest for the collision at the longest axis of the deformed nucleus, while the distance between mass centers is the largest. On the other hand, for a side collision the fusion barrier is high, while the distance is short. We investigated which collision tends to fuse these nuclei. The experimental result is shown in Fig. 1-4. It is found that the two nuclei fuse at a side collision, but not at a tip collision. The fusion probability for the collision between the projectile 82Se and the spherical target Ce is also shown for comparison in Fig. 1-4. It has been found that as can be seen in the collision between 82Se and Ce, the fusion probability becomes small for the reaction system where the charge product ZtZp of atomic numbers of projectile and target is around 2,000. This was the difficulty for the synthesis of heavy elements. We overthrew this established theory and found that when the projectile collides with the side of the deformed nucleus, the fusion probability becomes larger because of the close contact. We are studying further whether this advantage for fusion with deformed nuclei is also maintained for a heavier reaction system. |