1.5 Again, a Wonder in Uranium Compounds
–Two-Dimensional Conductivity Even in a Tetragonal Structure Uranium Compound


Fig. 1-8 Crystal structure and the magnetic structure of (a) UBi2 and (b) UX2 (X=Sb, As, P)

The crystal structure, which is long along the [001] direction, has a longer magnetic structure due to antiferromagnetism. Arrows indicate the directions of the magnetic moments which the uranium atoms have.

Fig. 1-9 Angular dependence of the de Haas-van Alphen (dHvA) frequencies of (a) UBi2 and (b) USb2

The dHvA effect is oscillations of magnetization when the magnetic field changes. The cross-sectional area of a Fermi surface can be calculated from the dHvA frequency. Solid lines are proportional to 1/costheta (theta is the angle with respect to the magnetic field) and as they are proportional to the cross sections of cylinders, the Fermi surfaces are cylindrical. alpha, beta,... indicate different Fermi surfaces.

Fig. 1-10 Experimentally detected Fermi surfaces of (a) UBi2 and (b) USb2

The cross-sectional areas of the Fermi surfaces are obtained from the dHvA frequencies and then the form and volume are calculated from the cross-sectional areas. The Fermi surface alpha of (a) is spherical and does not have a theta-dependence. Other cylindrical Fermi surfaces have a 1/cos theta-dependence.



Metals are good conductors of heat and their conductivity is due to the conduction electrons. The properties of metals are mainly due to the nature of the conducting electrons. Fermi surfaces show the space distributions of the conducting electrons' momenta. Fermi surfaces indicate the features of super-conductivity or electrical conductivity etc.
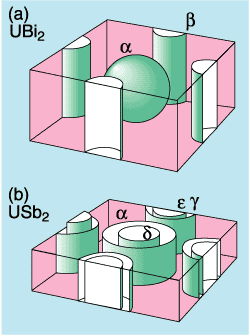
In UX2 (X=Bi, Sb, As, P), we found for the first time cylindrical two-dimensional Fermi surfaces in uranium compounds. For these two-dimensional Fermi surfaces, there are insulating layers between conducting layers, and it is a characteristic that conduction is largely anisotropic. The two-dimensional Fermi surfaces were previously found in cuprate high-temperature superconductors or organic conductors. It is easily understood from their crystal structures that such compounds have two-dimensional Fermi surfaces. By the way, the easiest example, which shows isotropic conduction, are the spherical Fermi surfaces of alkaline metal or copper.
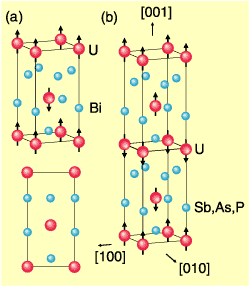
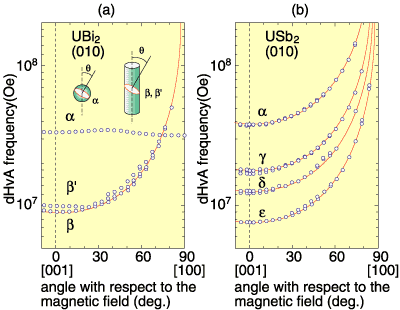
UX2 (X=Bi, Sb, As, P) have tetragonal crystal structures with a long length along the [001] direction and so it seems to be difficult to think that they have two-dimensional conduction (Fig. 1-8). Figure 1-9 shows the experimental result that there are cylindrical two-dimensional Fermi surfaces. These compounds show antiferromagnetic ordering near room temperature (180 - 280K). UX2 (X=Sb, As, P) especially have magnetic structure with a double unit cell and then the magnetic structure becomes much longer along [001] (Fig. 1-8). Thus, the reciprocal lattice of the crystal (the reciprocal lattice corresponds not to distance but to momentum, and the length of the reciprocal lattice is inversely proportional to the length of the real crystal lattice) or the Brillouin zone becomes half of that in the paramagnetic state. It is very flat along [001] (Fig. 1-10). Namely, the Fermi surfaces in the paramagnetic state are cut in half along [001] and cylindrical Fermi surfaces appear.
Once again an unusual property viz., that two-dimensional Fermi surfaces appear due to the antiferromagnetism, becomes obvious.


Reference
D. Aoki et al., Crystal Growth and Cylondrical Fermi Surfaces of USb2, J. Phys. Soc. Jpn., 68(7), 2182 (1999).

Select a topic in left column


Persistent Quest-Research Activities 2000
Copyright(c)Japan Atomic Energy Research Institute