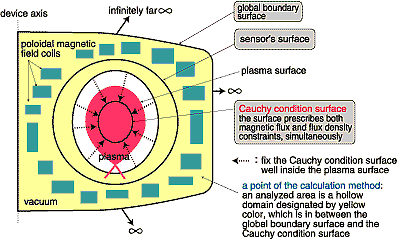
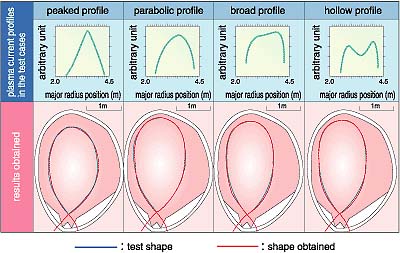
| Plasma is an aggregation of charged particles and has electromagnetic fields. The shape of plasma is obtained to diagnose the electromagnetic field. One of the methods to obtain the electromagnetic fields is to use a set of differential equations (examine the internal characteristics) with a separation of variables or finite element methods using some weighting and/or Green's functions. Another way is to use a set of integral equations (scrutinize external appearances). We need a lot of information in the plasma interior to get a solution by the differential equations, and it is not realistic to know all the necessary characteristics, while accuracy diminishes using approximations. The integral equations give, in principle, an exact solution with information only from the outside. However, in the case of poor convergence of an integrals, the solution becomes infinite and/or not unique. We tried to find new methods to get an exact solution of the plasma shape by the minimum external measurements of the electromagnetic field. We proposed a hypothetical surface, the so-called Cauchy condition surface, which satisfies universally the relation between the magnetic flux and flux density of the electromagnetic fields, and fixed it inside the plasma surface. When we put this quantity in the integral equations, we obtained the solution not only on the shape but also on the current profile, in a straightforward manner. Figure 2-12 shows the outline concept of the diagnoses. Typical examples of the identified results are shown in Fig. 2-13. |