When a large-scale computation for science and engineering is
carried out, the percentage of CPU time necessary for "numerical
calculations" such as the solution of simultaneous linear equations, eigenvalue
problems, Fourier transforms, and so on is overwhelmingly large
among all the processes of a program. In order to attain high
efficiency parallel computation, therefore, it is most important
to parallelize, particularly the numerical calculation programs.
Though even in many parallel computers numerical calculation libraries
are provided as in conventional large-scale computers, there are
scarcely standard numerical calculation libraries which can be
used efficiently and safely in a wide variety of different parallel
computers. This is because the differences between parallel computers
are enormous in comparison with those of conventional sequential
computers. In this situation we developed "a versatile numerical
computation library for parallel computers" on the basis of the MPI library, the defacto standard in the parallel
computation environment.
One of the most important features of this kind of library is
the fact that the execution speed of computation should be proportional
to the number of processors used for parallel computation as far
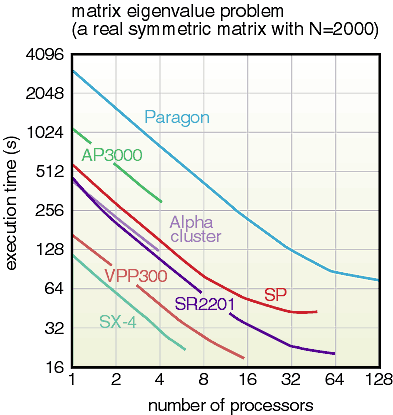
as possible. Figure 11-3 shows the computation time versus the
number of processors of the numerical computation program in the
library executed on various parallel computers in CCSE (Center
for Promotion of Computational Science and Engineering), JAERI.
It is clearly understood that the proportionality feature of the
computation speed is attained up to a large number of processors
irrespective of the inherent performance of each computer. Figure
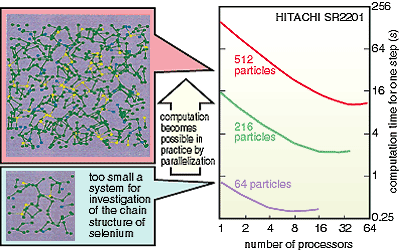
11-4 shows the result of a molecular dynamics simulation of the
structure of liquid selenium calculated using an eigenvalue analysis
program in the library which was developed. As the computation
time is extremely reduced by the parallelization, a simulation
of a large number of particles becomes realizable. |