Publication Date: December 19, 2025
Access counts:0
Numerical Methods of Interpolation on the Phase Space
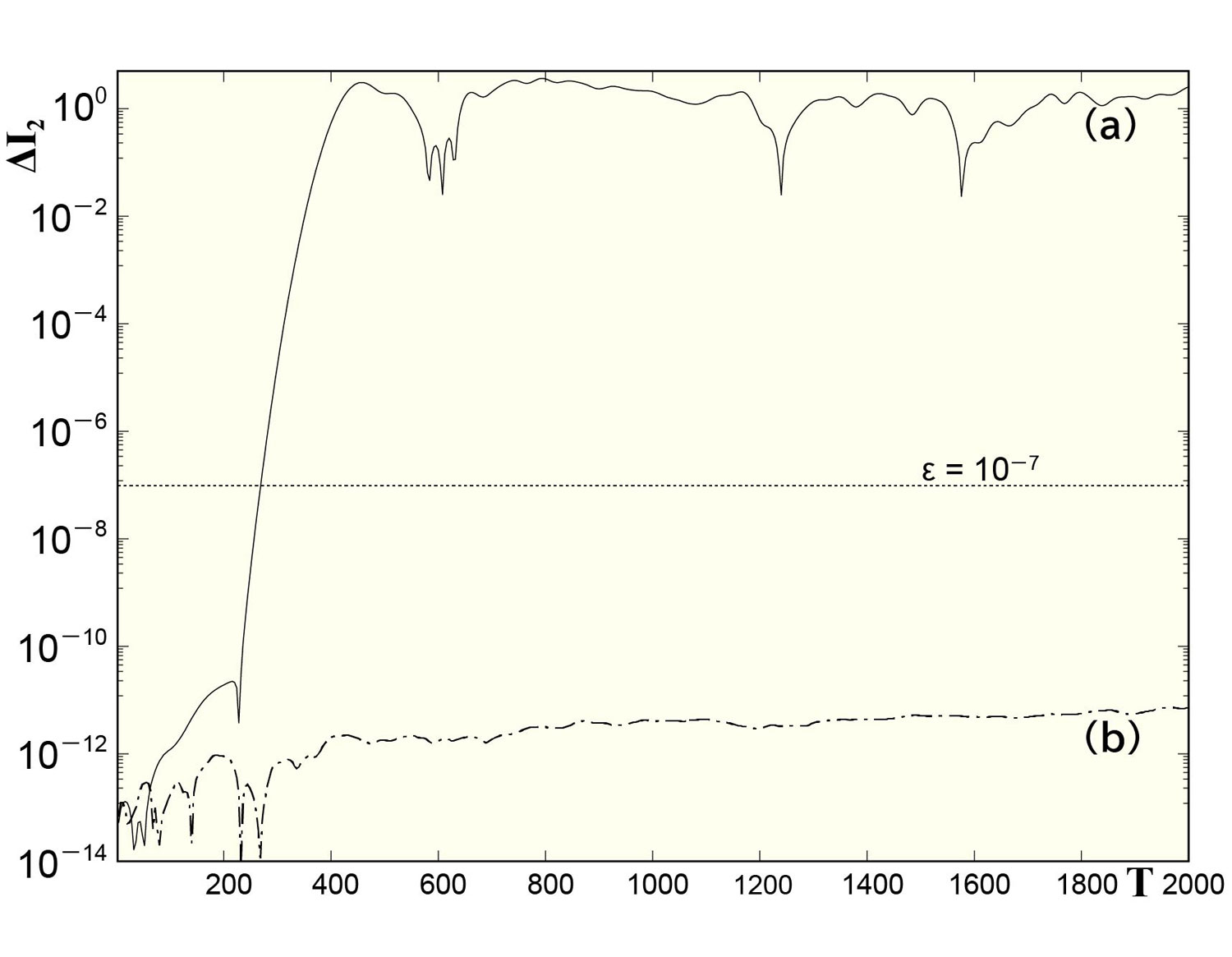
Fig. 1 Time evolution of deviation from initial value of the Poincare invariant
Theoretical research of materials at the atomic level is based on the numerical simulations of molecular dynamics. Therefore, there is a constant need for improvement of numerical methods that can solve the classical equations of motion accurately and effectively.
This research proposes a method for estimating microcanonical statistical mechanical quantities from a relatively small number of simulation data. However, since errors increase as the calculation time increases, we examine the validity of this method over a long period of time in this paper.
In calculating a statistical mechanical quantity (area in the phase space) that is inherently time-conserving in a simple test system (a Hamiltonian system with low degrees of freedom), we perform numerical simulations with minimal error up to T–200 (Fig. 1(a)). On the other hand, in a system in which low-degree-of-freedom Hamiltonian systems are connected by weak linear springs, we find that our method is effective over a relatively long period of time (T–2000) (Fig. 1(b)).
Based on the results, we will study various ideas to extend the effective time period of our simulation method in the future works.
If you have any comments or feedback about this page, please click the button to share your thoughts with us.
