All matter in this universe is made by assemblies of the so-called Fermi particles, which obey Fermi statistics (Fig.10-5). Therefore, if one precisely identifies the dynamics of interacting Fermi-particles, the properties of that matter are in principle predictable from microscopic to macroscopic levels. Once Schrödinger, a founder of quantum mechanics, succeeded in describing the quantum mechanics via the Schrödinger Equation, some physicists immediately jumped to a conclusion that physics will be completed soon. The reason is that they believed that the all matter would become understandable by a big computer solving Schrödinger Equations for quantum many-body systems. However, this understanding was not attained within the 20th century. Instead, physicists have made their efforts to create approximation techniques and tried to understand Fermi particles behaviors by using them.
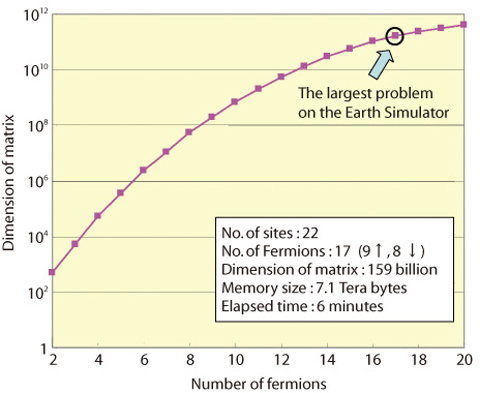
On the other hand, the question, what is the largest number of quantum bodies whose system can be solved, has recently become an interesting issue since successively larger supercomputers have been developed. Thus, we attempted to solve a problem of atomic Fermi gas on the Earth Simulator, and succeeded in solving the ground state of 17 fermions loaded on 22 sites of an optical lattice (Fig.10-6). This problem is equivalent to a mathematical one calculating the eigenstate of a 159 billion dimensional matrix, which is one of the largest matrices ever solved to humankind. By adopting a new algorithm and taking advantage of specific architectures in the Earth Simulator, we were able to solve this problem within only 6 minutes. To our knowledge, there have been no studies of 20 fermion problems whose solutions were found on the order of minutes. Our calculation is the largest ever, and likely is the limit worldwide at present. In the future, further advancements of computers should enable to solve still larger matrices. Our new tasks will follow upon computer advancements.