10-6 Phase Property and Interaction Force of Pulsating Multiple Bubbles

- Existence of an Unknown Characteristic Frequency Is Confirmed -

Fig.10-8 Numerical simulation of pulsating, interacting bubbles
Fig.10-8 Numerical simulation of pulsating, interacting bubbles

When sound is applied, a bubble begins to pulsate. If several bubbles exist, an interaction force which can be either attractive or repulsive acts between the bubbles. In this simulation, an attractive force appears. Two pulsating bubbles gradually approach each other and finally collide to merge (temporal sequence from the upper left to the lower right).

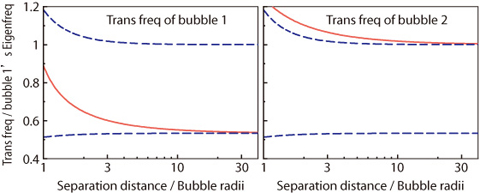
Fig.10-9 Transition frequencies of two interacting bubbles as functions of the distance between the bubbles

Fig.10-9 Transition frequencies of two interacting bubbles as functions of the distance between the bubbles

The blue lines denote the resonance frequencies and the red lines correspond to the transition frequencies that we have discovered. Though in a frequently cited explanation the direction reversal of the interaction force occurs at the resonance frequencies, in our theory it occurs around the characteristic frequencies we found.

Bubbles in a liquid are familiar objects to us. One can easily produce and observe many bubbles by shaking a water-filled bottle. Bubbles are significant in diverse fields including engineering and medicine. Microbubbles injected into blood vessels are used as ultrasound contrast agents; cavitation bubbles emerging in a depressurized liquid have a strong impact force that damages fluid machinery in nuclear plants; sonoluminescencing bubbles which emit light in a strong sound field are utilized as a chemical reactor. Also, the innumerable bubbles forming whitecaps on the ocean are assumed to have an effect on climate.

Despite their familiarity, bubbles still have many unsolved problems. Recently, by examining theoretically and numerically the pulsation phases of bubbles pulsating and interacting with each other in a sound field (Fig.10-8), we have found an unknown characteristic frequency (Fig.10-9). The characteristic frequency, which we call "transition frequency," inverts a bubble's pulsation phase (e.g., from in phase to out of phase with the driving sound) without resonance, and is thus essentially different from the resonance frequency.

We have also found that several unsolved problems of bubbles are resolved by our discovery. One of them is the mechanism of an interaction force acting between pulsating bubbles. It had already been known that the force changes its direction depending on whether phase differs between the bubbles and can thus be either attractive or repulsive. However, there has not yet been an established theory on the underlying mechanism of the direction reversal. We have found out that the transition frequency is precisely the factor determining this direction; that is, when one changes the frequency of the driving sound, the interaction force inverts its direction when the frequency passes through the transition frequency. This discovery questions the frequently cited explanation that the direction reversal occurs at the resonance frequency.

We are now performing additional investigations to fully confirm the existence of the transition frequency. The results given in this study will be useful tools for understanding phenomena observed in systems involving many bubbles, such as the collapse of cavitation bubble clusters and stable structure formation through bubbles. This work was partly supported by MEXT through a Grant-in-Aid for Young Scientists (B) (No. 17760151).

Reference
Ida, M., Phase Properties and Interaction Force of Acoustically Interacting Bubbles: A Complementary Study of the Transition Frequency, Physics of Fluids, vol.17, no.9, 2005, p.097107-1-097107-13.

 |