1-1 Handling Nuclear Data Accurately and Efficiently

- Lattice Calculation Code Combining Ultra-Fine and Fine Group Calculations -

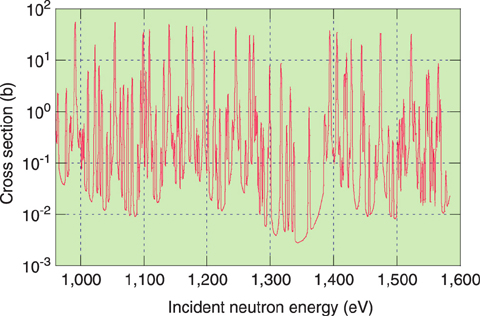
Fig.1-2 Energy dependence of 238U capture cross section

Fig.1-2 Energy dependence of 238U capture cross section

 

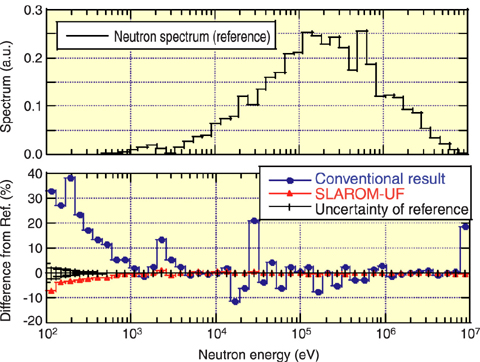
Fig.1-3 Analysis accuracy of neutron spectrum of "JOYO" MK-I core

Fig.1-3 Analysis accuracy of neutron spectrum of "JOYO" MK-I core

Neutron spectra in an infinite lattice calculation using SLAROM-UF and using the conventional method are compared with regard to the difference from the reference (a continuous Monte Carlo calculation shown in the upper half). Use of SLAROM-UF almost eliminates the difference.

 

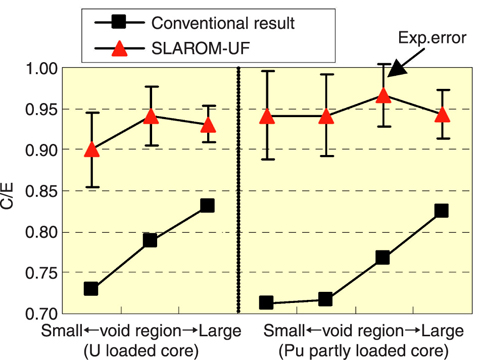
Fig.1-4 A ccuracy of sodium void reactivity analysis of criticality experimental data

Fig.1-4 A ccuracy of sodium void reactivity analysis of criticality experimental data

The experimental data on BFS criticality experiment simulating Russian fast reactor BN-600 is analyzed. Use of SLAROM-UF improves the C/E ratio, thus reducing the regional dependence of the data.

In fast reactor analyses, it is important to evaluate neutron reactions accurately over the energy range from 100 eV to several MeV, where neutron cross sections have resonances at certain energies, where the probability of neutron reactions fluctuates rapidly (Fig.1-2).

In a conventional method, a discrete 70-group cross section set has been used, and effects of resonances are tabulated in advance. This method causes several dozen percent error in a sodium void reactivity analysis. Furthermore, the constants used were optimized to a specific reactor type of "MONJU", so that errors occur depending on core sizes, etc.

There is a continuous energy Monte Carlo code free from error; however, it is not suitable either for calculations of very small values of the sodium void reactivity or for a detailed physical investigation.

Thus, we developed a code based on a deterministic method with accuracy comparable to the Monte Carlo code. The basic idea of the code is a combination of two kinds of calculations: an ultra-fine group (UF) calculation (approx. 100,000 groups) and a fine group calculation (max. 900 groups). The UF calculation covers the energy range below about 50keV where resonances are remarkable. Its group structure is so fine as to distinguish each resonance. Effective cross sections are efficiently created by solving a slowing down equation focusing only on elastic scattering and absorption. The fine group calculation follows the conventional method except for use of the effective cross section created in the UF calculation and use of a sufficiently fine energy structure above the 50keV that resonances of structural materials can be treated accurately.

Performances of the developed code SLAROM-UF are shown in Fig.1-3 and Fig.1-4. SLAROM-UF gives accuracy comparable to a continuous energy Monte Carlo code, and a drastic improvement is observed in its agreement with experimental values as well.

SLAROM-UF has the capability of the conventional calculation and can be used either for a rough or a very detailed calculation, depending on accuracy required. It has already been used in the analysis of "MONJU".

Reference
Hazama, T. et al., Development of a Fine and Ultra-Fine Group Cell Calculation Code SLAROM-UF for Fast Reactor Analyses, Journal of Nuclear Science and Technology, vol.43, no.8, 2006, p.908-918.

 |