3-3 Sharpening Plasma Shape Improves Pressure Limit

- Stabilization of the Edge Localized Mode by Sharpening the Plasma Shape -

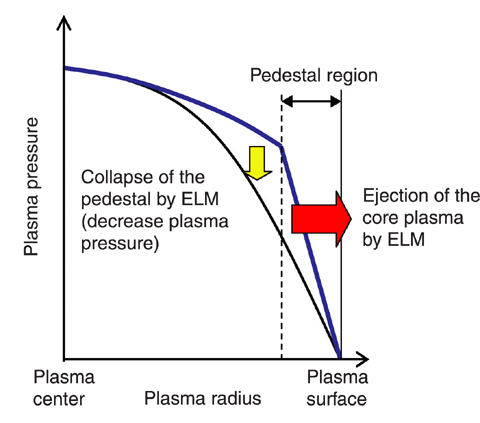
Fig.3-7 Pattern diagram of the collapse of the edge pedestal structure in the edge localized mode (ELM)

Fig.3-7 Pattern diagram of the collapse of the edge pedestal structure in the edge localized mode (ELM)

The pedestal structure of the plasma pressure (blue line) will collapse when the pressure becomes too high and the edge localized mode (ELM) is generated. After such a collapse, the pressure profile becomes smooth.

 

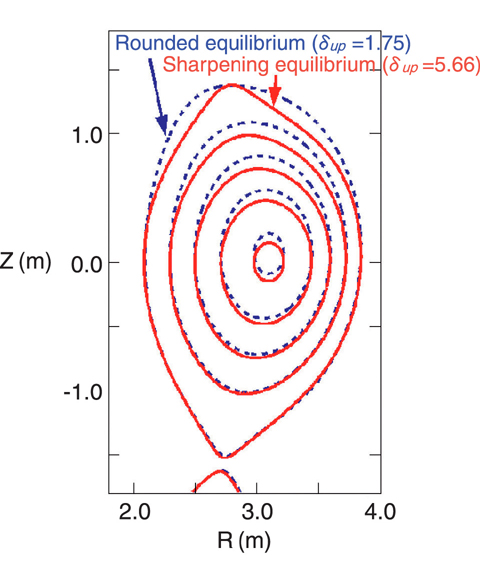
Fig.3-8 Plasma cross-sections of the equilibria whose sharpness are different

Fig.3-8 Plasma cross-sections of the equilibria whose sharpness are different

We investigated numerically the ability of equilibria whose sharpness at the top of the cross-section are different to prevent the unstable peeling- ballooning mode. (The parameter δ up expresses the sharpness. This parameter increases as the cross-section becomes sharper.)

 

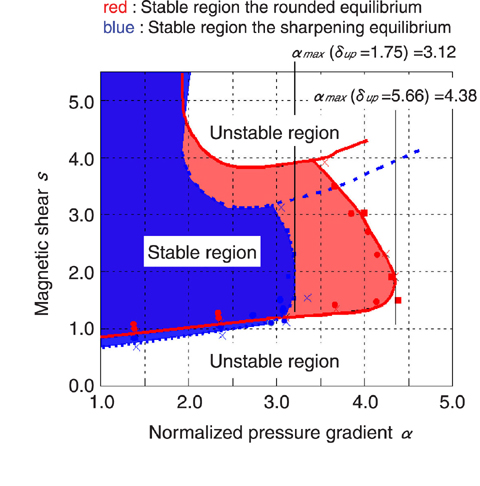
Fig.3-9 Expansion of the MHD stable region by increasing the sharpness

Fig.3-9 Expansion of the MHD stable region by increasing the sharpness

MHD stability diagram on the plasma pressure gradient and the magnetic shear plane. The stable region expands as the sharpness increases from δ up=1.75 (blue region) to 5.66 (red region). This expansion improves the maximum pressure gradient at which stability can be maintained by over 30%.

From the economical point of view, a fusion reactor needs to confine high pressure plasma stably. The so-called "H-mode plasma" whose plasma pressure exhibits a pedestal structure near the plasma surface (Fig.3-7) is desirable to increase the total plasma pressure. However, when the pressure of this pedestal region becomes too high, an instability called the edge localized mode (ELM) sometimes induces the collapse of the pedestal structure. This collapse ejects the high temperature plasma to the outside of the confined region, and it decreases the total pressure of the confined plasma. Therefore, understanding the conditions which stabilize ELM is an important issue for high pressure plasma.

Previous studies revealed experimentally and theoretically that a large collapse near the plasma edge is induced by the Type-I ELM, which is one of the ideal magnetohydrodynamic (MHD) instabilities called peeling-ballooning mode, and this MHD mode can be stabilized by changing the plasma cross-section from circular to "D-shape" . However, the impact of the "D-shaping" on the ELM stability changes in different experimental devices. This result implies that the stability of this MHD mode will depend on not only the "-shaping" but also other shaping effects.

To investigate these shaping effects, we developed the linear ideal MHD stability code MARG2D, and analyzed the effect of the sharpness near the top of the plasma surface (Fig.3-8) on the stability of the peeling-ballooning mode. As a result, we reveal that the peeling-ballooning mode can be stabilized by sharpening the plasma top shape, even when the ellipticity and the triangularity, which are the shaping parameters to express the "D-shape" of the cross-section are almost unchanged. This stabilization increases the maximum pressure gradient at which stability can be maintained. For example, by changing the plasma top shape as shown in Fig.3-8, the maximum pressure gradient increases over 30% as shown in Fig.3-9. Moreover, we found this stabilization is caused by increasing near the top of the plasma the magnetic shear - the change of the direction of the magnetic field line from the center to the surface of plasma.

This experimentally verified stabilizing effect of the sharpness in JT-60U is theoretically explained in this study. Based on this result, greater plasma performance can be realized in ITER and JT-60SA.

Reference
Aiba, N. et al., Effects of “Sharpness” of the Plasma Cross-section on the MHD Stability of Tokamak Edge Plasmas, Nuclear Fusion, vol.47, no.4, 2007, p.297-304.

 |