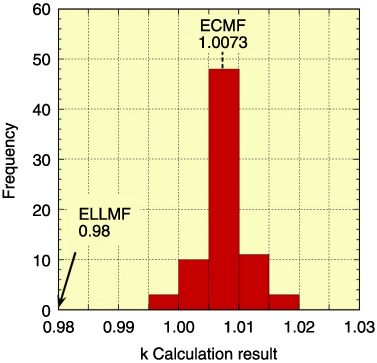
Fig.6-18 Distribution of critical benchmark calculation results (homogeneous low-enriched uranium system)
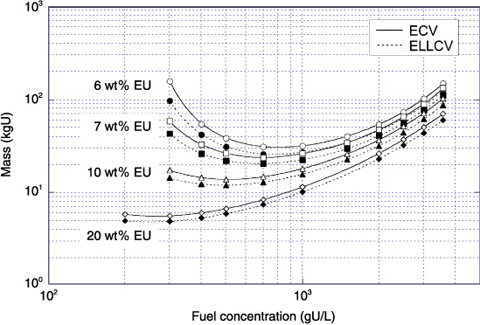
Fig.6-19 Critical mass data for homogeneous ADU(II)-H2O (with water reflector)
Fission chain reactions linked by neutrons are maintained in a nuclear reactor by keeping its nuclear fuel critical, and energy and radiation emitted from the reaction are utilized. The nuclear fuel must not, however, be critical in places other than a nuclear reactor. Safety management for this purpose is generally known as criticality safety.
Due to advances in computation technology, it has become feasible to analyze nuclear interactions between neutrons and nuclei in materials such as nuclear fuel, and to judge with pretty good accuracy if a condition is critical, wherein a fission reaction can continue, or is safely sub-critical. The analysis computes the effective neutron multiplication factor k, which is the ratio between the neutron production rate by fission and the annihilation rate by absorptions, etc. Theoretically, k= 1 and k< 1 indicate criticality and sub-criticality, respectively. It is indispensable to know the accuracy quantitatively before practical applications of the analysis method; therefore a validation was conducted for a combination of the continuous energy Monte-Carlo code MVP and the nuclear data library JENDL-3.2, both of which were developed in Japan.
A validation needs critical masses of various nuclear fuels measured in critical experiments as references. The data used for the present validation came from the database of the International Criticality Safety Benchmark Evaluation Project (ICSBEP) of OECD/NEA. The results of critical mass measurements conducted in many countries are registered in the database; conditions such as the kinds, structures, and dimensions of nuclear fuels that became critical are described in detail for each measurement.
Analysis based on this information gives distributions of k around 1 as shown in Fig.6-18, which may be caused by uncertainties in the ICSBEP data and the nuclear data library. The important fact is that a case may be critical in reality even if the computed k is < 1. If, however, a value sufficiently smaller than the lowest limit in the distribution is chosen as the Estimated Lower Limit Multiplication Factor (ELLMF) klim, and if the computed k is < klim, then it can be judged as being actually sub-critical. A statistical test of the distribution concluded that the value 0.98 could be employed as klim. This is a good improvement on the value 0.95 employed for the analysis method approximately two decades ago.
Moreover, the minimum mass, dimensions, concentrations, etc., of various nuclear materials whose ks are 1 and 0.98 were computed with the same method, and published as a revised data collection for the nuclear criticality safety handbook, to be used as references for designing equipment and procedures to handle nuclear fuel. The new version has become more useful than the old one by adding new kinds of data, as shown in Fig.6-19, for example.