10-1 Determination of Properties of Nuclear Fuels through Numerical Simulation

－First-Principles Calculations of Electronic States of Plutonium Dioxide－

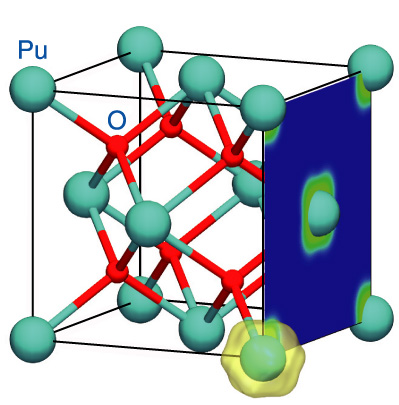
Fig.10-2　Crystal structure of plutonium dioxide and charge density resulting from the presence of f-electrons

Fig.10-2　Crystal structure of plutonium dioxide and charge density resulting from the presence of f-electrons

The light-blue and red spheres correspond to plutonium and oxygen atoms, respectively. The charge density of f-electrons is depicted in the right-side plane, where the density increases from blue to yellow. The yellow surface around the right lower Pu atom represents the isosurface of the charge density. The charge density is calculated by considering strong correlations and spin-orbit couplings.

 

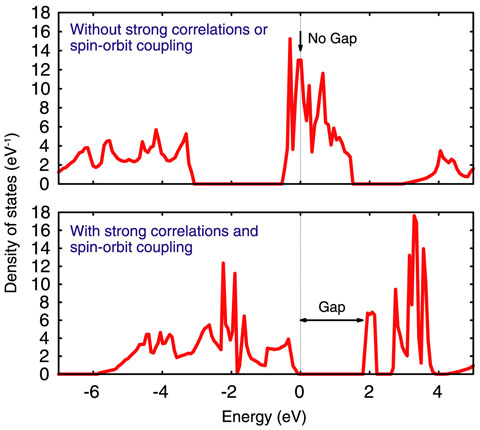
Fig.10-3　Density of states of plutonium dioxide (PuO2)

Fig.10-3　Density of states of plutonium dioxide (PuO2)

The upper panel shows the density of states (DOS) calculated without strong correlations or spin-orbit couplings, and the lower panel shows the DOS obtained by considering strong correlations and spin-orbit couplings. In the upper panel, PuO2 is considered to be metallic because the DOS with zero energy does not vanish. In the lower panel, the DOS above zero energy has a gap, and therefore, this material is an insulator. Note that the zero energy point corresponds to the Fermi energy.

In order to develop more secure and more efficient nuclear fuels, we have to have a detailed knowledge of the properties of candidate fuels. However, the determination of the properties through experiments is not easy owing to limitations associated with the handling of nuclear materials and the difficulty in reproducing the high-temperature conditions in nuclear reactors. In such cases, simulations are effective for the evaluation of the properties of nuclear fuels.

Although there are various simulation methods to evaluate material properties, recently, first-principles calculations have come to be very often used. First-principles calculations are considered to be the most reliable method since they use fundamental information only about the interactions of electrons and atoms and need no empirical parameters. However, this method has failed when used for the computation of the electronic states of plutonium dioxide (PuO2) (Fig.10-2). Specifically, the failure is that the first-principles calculations predict a metallic state of PuO2 as the ground state, while measurements indicate an insulating state. For a while, the reason for this failure had been believed to be the lack of strong correlations in first-principles calculations; strong correlations are important in the interactions between so-called “f-electrons” in Pu atoms. However, it was recently reported that first-principles calculations with strong correlations also fail to reproduce the insulating state. We then explored other reasons for the failure. We found that spin-orbit couplings are also necessary to reproduce an insulating state. Although it is known that spin-orbit couplings play a significant role in large atoms such as Pu, they have often been neglected in calculations for PuO2 so far. We succeeded in reproducing the insulating state by considering both strong correlations and spin-orbit couplings (Fig.10-3).

For the development of new nuclear fuels, information about more complex properties, such as thermal conductivity, and reactions under extreme situations is necessary. In order to obtain the information through simulations, large-scale computing is crucial. In such large-scale computing, reliable results can be achieved by using first-principles calculations. Our success in reproducing the insulating state of PuO2 by using first-principles calculations is expected to form the basis for the evaluation of more complex properties of nuclear fuels.

Reference
Nakamura, H. et al., Effects of Spin-Orbit Coupling and Strong Correlation on the Paramagnetic Insulating State in Plutonium Dioxides, Physical Review B, vol.82, issue 15, 2010, p.155131-1-155131-6.

 |