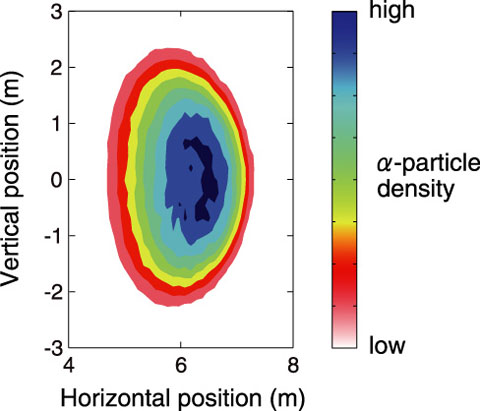
Fig.3-18 Density distribution of isotropically born α-particles
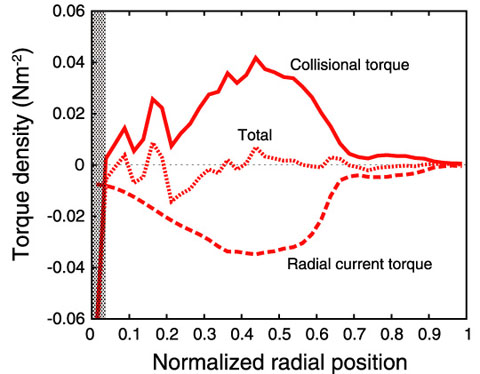
Fig.3-19 Radial profile of torque density induced by α-particles
In order to sustain high-pressure fusion plasma, various instabilities inherent to the plasma must be suppressed. One of the potential methods for suppressing such instabilities involves rotating the plasma in the toroidal direction. In current tokamak experiments, neutral beam injection (NBI) can be used for efficiently applying a torque to the plasma via the formation of fast particles, thus enabling rotation control. However, in future fusion reactors, the effective torque generated by NBI may not be very large; hence, much attention has been paid to the possibility of intrinsic torque generation by fusion-born α-particles.
The torque produced by fast particles is the sum of the collisional torque generated by collisions between fast thermal particles and the radial current torque resulting from the motion of fast particles in a magnetic field. Unlike directional fast particles formed by NBI, α-particles are born isotropically (Fig.3-18), and hence, they are never believed to produce any kind of torque. The orbit-following Monte Carlo code (OFMC) for fast particles has been recently updated to incorporate a mechanism for accurately estimating the radial current torque, and the updated OFMC has been used to analyze the behavior of α-particles in a DEMO-relevant plasma. Here, DEMO (DEMOnstration power plant) denotes a prototype fusion reactor. The analysis reveals that the centrally peaked birth profile of the α-particles shows both finite collisional and radial current torques. The magnitude of these torques seems to be comparable to that of the torque due to NBI, but the collisional torque acts in the direction parallel to the plasma current, whereas the radial current torque acts in the opposite direction. Because of this mirror symmetric characteristic of the profiles, the two torques cancel out each other, and the net torque is zero (Fig.3-19). This finding implies that in a perfectly axisymmetric tokamak, the α-particles cannot produce the intrinsic torque by themselves, consistent with the law of conservation of canonical angular momentum.
However, this fact also indicates that a net torque must arise in an actual, slightly asymmetric tokamak reactor with finite toroidal-field coils that create a toroidal magnetic field ripple (bumpiness). The ripple tends to accelerate the radial transport of fast particles, leading to an increase in the radial current torque. Thus, the balance in the torque in an ideal axisymmetric system will be violated in an actual system, and a net counter torque will be generated. Accurately calculating this torque is indispensable for estimating the additional torque required for inducing toroidal rotation that helps in suppressing plasma instabilities.