5-2 High-Power γ-ray Generation via the Radiation Reaction Effect Using an Ultra-Intense Laser Pulse

－Proposal for a New Laser-Driven γ-ray Source－

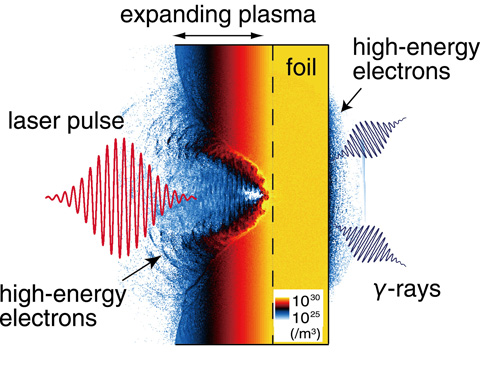
Fig.5-5　Simulation results showing the electron density distribution of a solid target irradiated by an intense laser pulse in the unit of m-3

Fig.5-5　Simulation results showing the electron density distribution of a solid target irradiated by an intense laser pulse in the unit of m-3

Expanding plasma, which is generated by a prepulse, exists in front of the foil. High-energy electrons escape from the target front and back side, and γ-rays are emitted from the rear side.

 

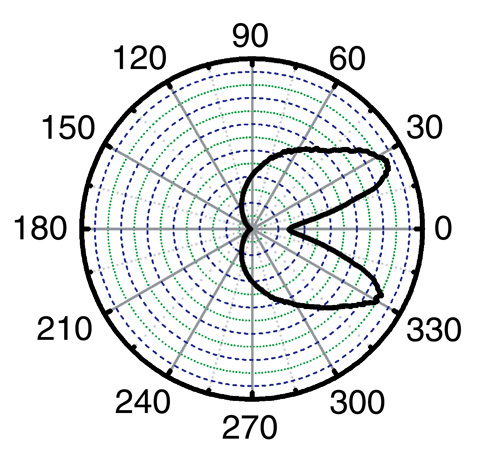
Fig.5-6　Angular distribution of the emitted γ-rays

Fig.5-6　Angular distribution of the emitted γ-rays

The γ-rays are collimated toward the laser propagation direction (The laser propagation direction corresponds to 0°).

 

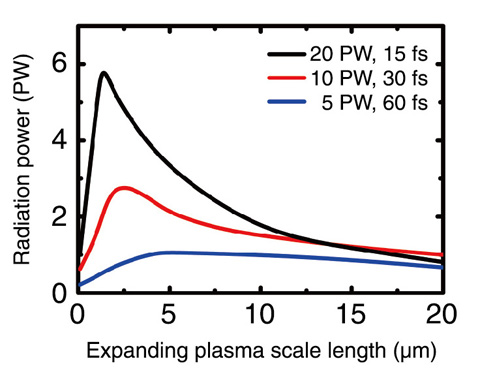
Fig.5-7　Dependence of the γ-ray power on the plasma scale length

Fig.5-7　Dependence of the γ-ray power on the plasma scale length

The three lines correspond to different laser power with a fixed laser energy. There exists an optimum scale length for effective γ-ray generation.

The radiation reaction (RR) effect, which is a back reaction acting on a charged particle that emits radiation due to its acceleration, is important such as for electrons in synchrotron accelerators or high energy charged particles in the universe. For electrons irradiated by an intense laser pulse, the RR effect has been neglected to date, but as laser intensities increase beyond approximately 1023 W/cm2, it is expected to play an important role. The power working on electrons by the RR effect can be easily estimated for a single electron performing a simple trajectory, but for plasmas, in which a collective behavior is important, it is not fully understood.

In this study, we used a newly developed particle simulation code incorporating the RR effect, which enables us to evaluate the amount of energy transferred from the laser pulse to γ-rays through the motion of electrons via the RR effect.

Fig.5-5 shows the electron density distribution of a thin-layer carbon target irradiated by a 10 PW, 30 fs laser pulse from the left hand side. The maximum energy of the accelerated electrons reaches 400 MeV, and some portion of them interact with the laser pulse and emit γ-rays. The pulse duration of the γ-ray is as short as the laser pulse, and the total energy is 96 J which is 32% of the incident laser pulse, resulting in a γ-ray power of 2.8 PW which is much higher than those generated by any other devices. The angular distribution of the emitted γ-rays is shown in Fig.5-6. The γ-rays are collimated toward the laser propagation direction into two lobes. The average γ-ray photon energy is 1.1 MeV, and the total photon number is estimated to be 5.5×1014.

The γ-ray characteristics depend on the laser and plasma parameters, such as the laser intensity, duration, and scale length of the expanding plasma. The γ-ray power dependence on these parameters is summarized in Fig.5-7, where the three lines correspond to different laser powers with a fixed laser energy of 300 J. The γ-ray power increases with the incident laser power and has an optimum value of the plasma scale length which is roughly the same as the laser pulse length. We have also revealed the dependences of the total photon number and the average photon energy on these parameters, which could lead to the possibility of controlling the γ-ray characteristics.

In conclusion, we have shown that γ-rays are generated by an intense laser pulse and solid target via the RR effect. This γ-ray source has high power, which is several orders of magnitude higher than those generated by other devices. The unique laser-driven γ-ray source could open up various new applications, such as laboratory astrophysics, photonuclear reactions, copious generation of electron-positron pairs.

Reference
Nakamura, T. et al., High Power γ-ray Flash Generation in Ultraintense Laser-Plasma Interactions, Physical Review Letters, vol.108, issue 19, 2012, p.195001-1-195001-5.

 |