Fig.9-10 Schematic of tokamak plasma (donut-shaped)
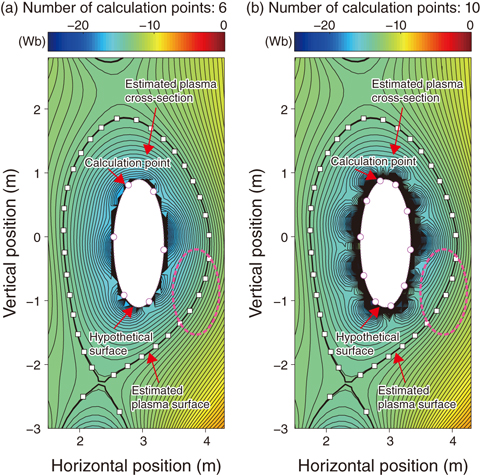
Fig.9-11 Plasma-cross-section shape estimated by the plasma-shape-estimation system
) and estimated by the plasma-shape-estimation system increases if the number of calculation points (
) arranged along a hypothetical surface increases from (a) 6 to (b) 10.
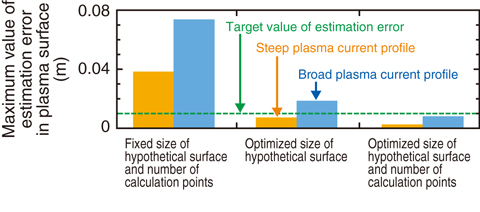
Fig.9-12 Estimation errors by optimizing the size of the hypothetical surface and the number of calculation points
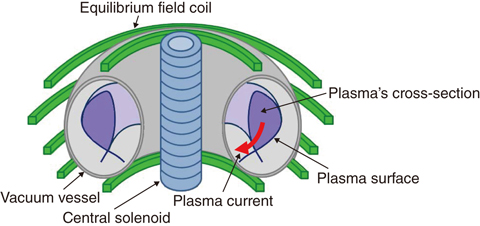
In order to maintain steady high-performance tokamak plasma and to prevent it from contacting structures such as the vacuum vessel (VV) and the like, it is necessary to control the plasma’s cross-sectional shape accurately (Fig.9-10). Since this shape is determined by the interrelation between the magnetic field generated by current flowing in the plasma (plasma current) and current sources other than plasma, it can be controlled by operating the currents for the central solenoid and equilibrium field coils used for controlling the plasma current and cross-sectional shape. However, it is necessary to estimate an accurate cross-sectional shape from the signals for the measurements arranged outside the plasma using a plasma-shape-estimation system to control the cross-sectional shape accurately. The plasma-shape-estimation system based on the Cauchy-condition surface (CCS) method was used for the JT-60U plasma cross-sectional-shape control. A hypothetical surface that plays the same role as the current flowing in the plasma is placed well inside the plasma, and the plasma surface can be estimated speedily and with high accuracy by calculating conditions on the hypothetical surface from the coil currents and by measurement signals. In order to apply the plasma-shape-estimation system based on the CCS method to the JT-60SA plasma-cross-section shape control, it is necessary to predict the estimation accuracy of the plasma surface in JT-60SA.
The accuracy of the plasma surface estimated by the plasma-shape-estimation system has been assessed by preparing the coil currents and measurement signals in reference to the plasma information simulated by the calculation code. The plasma surface estimated by the plasma-shape-estimation system is compared with the standard one produced by the calculation code. Although various plasma shapes are easily exhibited again if the number of calculation points arranged along the hypothetical surface increases, the estimation error in the plasma shape becomes large (Fig.9-11). In contrast, this quantity decreases if the size of the hypothetical surface increases because the hypothetical surface and the plasma surface are brought close together.
By assessing the estimation error in the plasma surface on various shapes and profiles of the plasma while changing the size of the hypothetical surface and number of calculation points, the relation expression between the size of the hypothetical surface and number of calculation points for minimizing the estimation error is determined. The estimation errors for the plasma having a broad current profile are larger than those for the plasma having a steep current profile, but they remain within the target value of 1 cm according to the relation expression (Fig.9-12). It is shown that the estimation accuracy is largely improved by optimizing the size of the hypothetical surface and the number of calculation points in JT-60SA and future fusion reactors on with a high elongation and triangularity of the plasma shape. This is an important result for achieving stable plasma-cross-sectional shape control in JT-60SA and future fusion reactors.
(low resolution PDF :299 KB) 