5-3　Realization of High-Intensity Proton Beams

－Beam-Instability Issues and the Measure at the 3-GeV RCS in J-PARC－

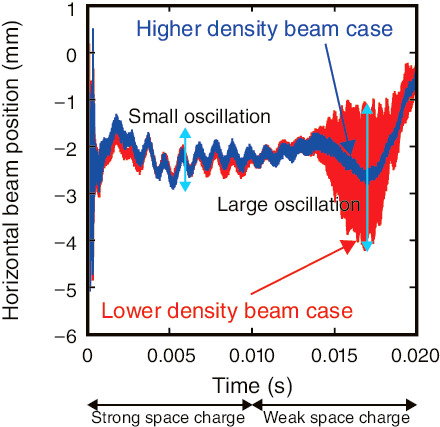
Fig.5-8 Measurement results of beam positions at the RCS

Fig.5-8 Measurement results of beam positions at the RCS

A bunch compression of only 2% makes an unstable beam (red) into a stabilized one (blue) by increasing the beam-current density.

 

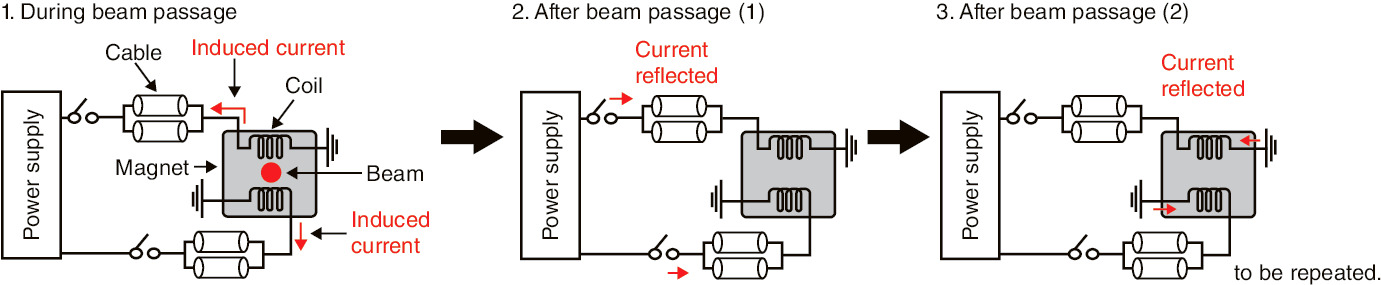
Fig.5-9 Schematic of beam-induced currents after a beam passes through the kicker magnet

Fig.5-9 Schematic of beam-induced currents after a beam passes through the kicker magnet

Beam-induced currents are superposed every time the beams pass through the kicker, because the power supply is switched off during the ramping time.

 

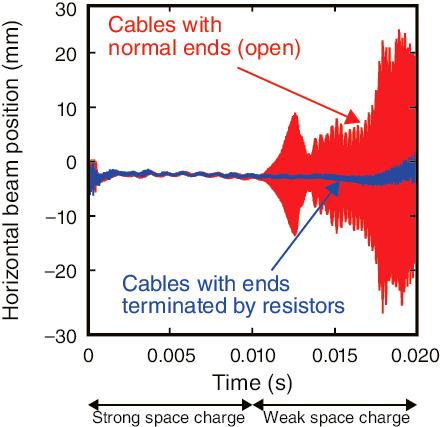
Fig.5-10 Dependence of beam positions upon terminal conditions

Fig.5-10 Dependence of beam positions upon terminal conditions

Termination of the cables’ ends with resistors improves the unstable beam (red) into a stabilized one (blue).

 

Over the past decades, the power frontier of proton accelerators has been advanced up to the 1-MW level; such high-intensity beams largely tend to oscillate transversely, making it quite difficult to accelerate the beam. This is the so called beam-instability issues; such instabilities are excited by the interaction between the beam and the chamber walls, or the devices in synchrotrons. Recently, we have developed two new beam-stabilization schemes against beam-instabilities.

Fig.5-8 shows measurement results for the 750-kW beam at the 3-GeV Rapid Cycling Synchrotron (RCS) in J-PARC. The oscillation after 0.010 s on the red line represents the beam instability.

The RCS is equipped with kicker magnets, which extract the 3-GeV beam by exciting a pulsed magnetic field with a 300 ns rising time. The magnets are installed in vacuum, and so tend to make the beam unstable during the ramping time. We have developed a new theory, and predicted that the beam-induced current on the kicker cables should be the dominant source of beam instability (Fig.5-9). Accordingly, we have demonstrated stabilization of the unstable beam by terminating the ends of the kicker cables with resistors, i.e., by suppressing the beam-induced currents (Fig.5-10). Furthermore, we have successfully stabilized the beam instability by avoiding the resonance condition between the beam-oscillation frequency and the reciprocating frequency of the beam-induced current in the cables, without modification of the kicker cables’ ends.

Our theory also predicts that the higher-energy beams tend to be unstable, due to mitigation of the space-charge-damping effect. As indicated by the red lines in Figs.5-8 and 5-10, the beam instability occurs at high energy, as expected. Finally, we successfully stabilize the high-intensity beam even after a ramping time of 0.010 s by compressing the beam length, i.e., by enhancing the space-charge-damping effects (the blue line of Fig.5-8).

These new schemes play an important role in establishing the beam-operation parameters toward the realization of a 1-MW-output beam power at the RCS.

Reference
Shobuda, Y. et al., Theoretical Elucidation of Space Charge Effects on the Coupled-Bunch Instability at the 3 GeV Rapid Cycling Synchrotron at the Japan Proton Accelerator Research Complex, Progress of Theoretical and Experimental Physics, vol.2017, issue 1, 2017, p.013G01-1-013G01-39.

 |