8-1　Quantifying the Radioactivity of Waste Products

－Accuracy Improvement of a Quantitative Method Focused on Scattering γ-rays－

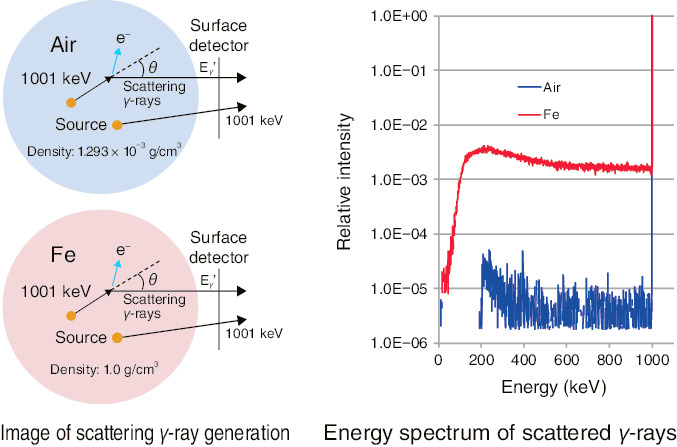
Fig.8-4 Simulation of γ-ray scattering

Fig.8-4 Simulation of γ-ray scattering

1001-keV γ-rays scattered from U progeny nuclides were determined using the transportation-calculation code MCNP. The shielding materials are composed of iron and air. The γ-ray spectra shielded with these components were calculated and compared with one another. Using scattered γ-rays over a wide range, the accuracy of the radioactivity determination was improved.

 

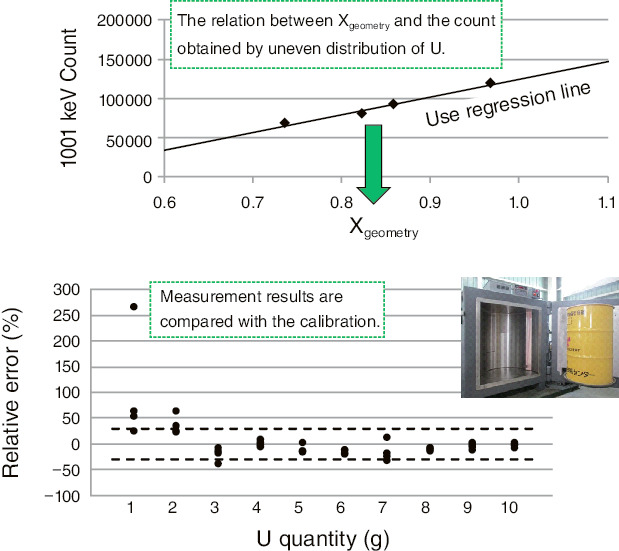
Fig.8-5 Relative error in radioactivity determination

Fig.8-5 Relative error in radioactivity determination

U (1–10 g) was placed in a simulated drum (200 kg). Two NaI detectors (3 × 5 × 16 inch) were used for measurement over a period of 1800 s. If the acceptable relative error is approximately ±30%, the lower limit of quantification was approximately 0.4 Bq/g, which is independent of the distribution of U sources. It seems that the radioactivity concentration below 1.0 Bq/g can be quantified, even if the error is included.

 

Dismantled materials generated from nuclear facilities are reused or disposed in repository sites. Confirmation of their radioactivity is required.

If confirmation of the clearance level of metal samples with complicated shapes were possible, the amount of waste could be reduced.

Even if wastes have complicated shapes, their radioactivity concentration can be measured by γ-ray measurement, since γ-rays have strong material-penetrating power.

Uranium (U) has a low γ-ray-emission rate. Therefore, increasing measurement efficiency is necessary. Semiconductor detectors have high resolution but low detection efficiency; hence, measurements with such detectors take a long time. To shorten the measurement time, it is reasonable to use a highly efficient NaI detector.

The shielding of γ-rays differs depending on the density of materials and the source localization. If the radioactivity concentration is evaluated by assuming that the density and source distribution of samples are homogenous, large errors will occur. For this reason, we estimated the attenuation due to the distance between the source and detector using measured values for two γ-rays (a, b) with different energies.

Let us consider the attenuation factor, Xgeometry. Here, let r be the distance from the source to the detector and µa,µb be the linear-attenuation coefficients of different energies of two γ-rays; the γ-ray counting rate, na, can be shown as na~e−µar/r2. In this case, ‘r’ in ln(na/nb)~−(µa−µb)r can be shown by the logarithm of the ratio of the counting rate. When the density distribution of the sample is regarded as homogeneous, the influence of different positions of sources is mainly expressed as 1/r2. When −ln(na/nb) is substituted for ‘r’, the Xgeometry can be expressed as follows (equivalent-model method):

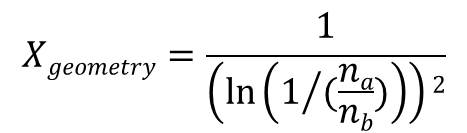
 Xgeometry


It is possible to replace the average distance between multiple source positions and detectors with one equivalent distance. A calibration curve is represented by the regression line calculated from Xgeometry and a counting rate of 1001 keV is obtained from a certain known amount of U. Comparing the plot obtained by measuring samples with the calibration curve, the U amount can be measured.

Though γ-rays of 1001 keV and 766 keV have been used for evaluation, the lower limit of quantitation of radioactivity was approximately 4 to 5 Bq/g (approximately 40 g of U) because of their low emission limits. Hence, we improved the accuracy of low-level radioactivity determination using scattered γ-rays with high counting rate (Fig.8-4). We tested our method with a simulated drum of 1.0 Bq/g or less using a commercially available device (Fig.8-5). In spite of the uneven distribution of the source, we were able to obtain a lower limit of quantification (below 1.0 Bq/g) required for the evaluation of the clearance level.

Reference
Yokoyama, K. et al., Verification of a Quantitative Method of Uranium238 in the Radioactive Waste using Photon Occurred by Compton Effect, Radioisotopes, vol.64, no.11, 2015, p.687-696 (in Japanese).

 |