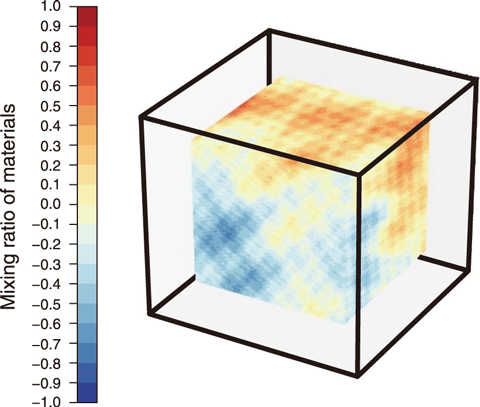
Fig.1-8 Nuclear system containing hypothetical fuel debris
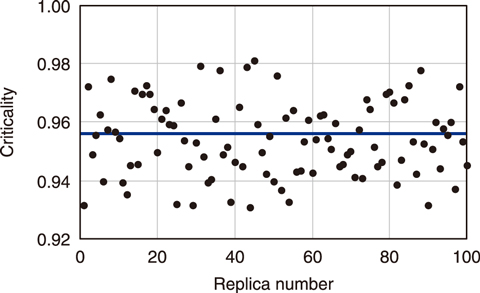
Fig.1-9 Fluctuation of criticality for a nuclear system containing hypothetical fuel debris
During the accident at the TEPCO’s Fukushima Daiichi NPS, fuel debris may have formed from melted nuclear fuels and structural materials such as iron and concrete. Estimating the criticality of nuclear systems containing fuel debris, important to prevent a criticality accident, can be done using computational models for the decommissioning project including defueling. In conventional models, the calculated geometry has been divided into regions small enough to be treated as uniform. However, applying these models to fuel debris systems is difficult, as the isotopic composition varies continuously in space. In addition, conventional analysis required an input of the composition over all regions, which is unknown in fuel debris systems.
As such, a new computational model was developed in which the isotopic composition varies continuously using the Weierstrass function. Users can generate a replica, as shown in Fig.1-8, by inputting the average value and dispersion of the composition and the parameters describing the randomness. Fuel debris is represented as a mixture of two materials, e.g., nuclear fuel and concrete, of which their ratio varies continuously in space. Since a replica is generated stochastically, each replica has a different isotopic composition distribution. Users can calculate the uncertainty due to the unknown distribution of the isotopic composition by calculating criticalities for multiple systems and performing statistical processing.
The resulting fluctuation of the criticality of a nuclear system containing hypothetical fuel debris is shown in Fig.1-9. A hundred replicas were generated and the criticality was calculated for each replica. The fuel debris was assumed to be a mixture of nuclear fuel and concrete (mixing ratio of 1:7) and included an average of 20% stainless steel. The content rate of stainless steel was assumed to vary randomly and continuously in space between 0% and 40%. In Fig.1-8, the brown region (scale of 1.0) shows the mixture at 0% stainless steel, whereas the blue region (scale of −1.0) shows the mixture with 40% stainless steel. The criticality of a nuclear system with uniform isotopic composition is shown as the blue line in Fig.1-9. One replicated case had a criticality of 0.98. This figure illustrates the importance of not only calculating the criticality for the uniform distribution but also estimating the dispersion due to the non-uniform distribution of stainless steel.
Future work will aim to develop a new model superposed with voxel geometry and the apply the model to a mixture of more than 3 materials to calculate the criticality for the various configuration of complex fuel debris systems. Future work will also involve the development of a Monte Carlo solver to implement and use the developed models easily.
This study was partly sponsored by the Secretariat of the Nuclear Regulation Authority (NRA), Japan.