3-4 Detection of the Singularity of Magnets Using Rotation

－Measuring the Angular Momentum Compensation, Key to Speeding Up Magnetic Devices－

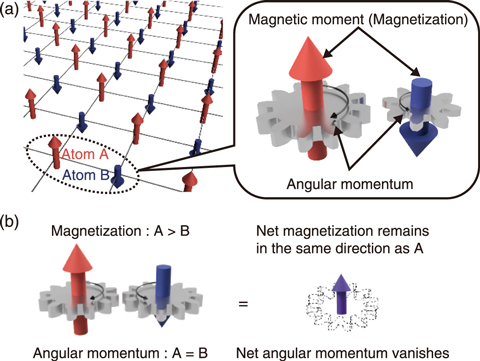
Fig.3-9

Fig.3-9 Schematic of a ferrimagnet

(a) Electric magnetic moments of atoms A and B are aligned in antiparallel. The magnetic moment of A is larger than that of B. (b) Net angular momentum vanishes at the angular momentum compensation temperature, but magnetization still remains.

 

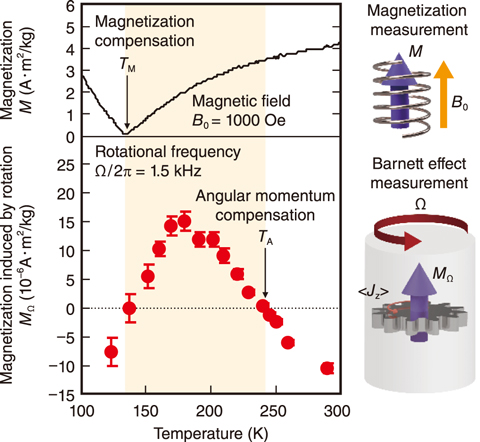
Fig.3-10

Fig.3-10 Magnetization and Barnett effect measurements

Usual magnetization measurements can only measure the magnetization compensation temperature. The Barnett effect determines the angular momentum compensation temperature as the temperature where the magnetization induced by rotation becomes zero.

 

The origin of magnetism in magnets is electron angular momentum. The electron has a spin angular momentum that corresponds to the rotation and an orbital angular momentum that corresponds to the orbital motion centered on the nucleus. These angular momenta cause a microscopic magnet, i.e., a magnetic moment. Magnetization appears due to the alignment of the magnetic moments within magnetic materials.

A ferrimagnet contains multiple types of magnetic atoms whose magnetic moments align in opposite directions, as shown in Fig.3-9(a). Here, the magnetic moment of A is larger than the magnetic moment of B, and as a whole, the north pole of the magnet is the same direction of the magnetic moment of A.

Some ferrimagnets have compensation temperatures, at which the magnetic moments or angular momenta of A and B compensate each other. At the magnetization compensation temperature TM, the net magnetization vanishes. At the angular momentum compensation temperature TA, the angular momenta of A and B compensate each other, but the net magnetization remains, as shown in Fig.3-9(b). However, conventional magnetization measurements have not been able to measure the angular momentum compensation temperature.

The Barnett effect was therefore used to determine the TA of the ferrimagnet Ho3Fe5O12; when a matter rotates, the angular momentum aligns in the rotational axis, thus magnetizing the matter. The measured temperature dependence of the magnetization induced by mechanical rotation is shown in Fig.3-10. The magnetization induced by rotation reaches zero at TA, as the Barnett effect does not work due to the net-zero angular momentum. Furthermore, TA was shifted to room temperature (293 K) by partial substitution of holmium (Ho) with dysprosium (Dy) in Ho3Fe5O12.

Magnetic memories store data in the magnetization direction and rewrite each bit by reversing the direction. For a normal magnet, the magnetization reverses with precession due to the angular momentum; precession prevents a smooth reversal of magnetization. On the other hand, the magnetization reverses at a high speed at TA, where the angular momentum disappears. Thus, TA has been attracting attention as a candidate for high-speed magnetic memories.

The developed technique to determine TA using the Barnett effect is expected to accelerate the search for materials applicable in high-speed magnetic devices.

This work was supported by JST ERATO Grant Number JPMJSK1402, and by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant-in-Aid for Scientific Research on Innovative Areas (Research in a proposed research area) (No.26103005), Grant-in-Aid for Scientific Research (A) (No.26247063), Grants-in-Aid for Scientific Research (B) (No.16H04023, No.17H02927), and by Grants-in-Aid for Scientific Research (C) (No.15K05153, No.16K06805).

(Masaki Imai)

References
Imai, M. et al., Observation of Gyromagnetic Reversal, Applied Physics Letters, vol.113, issue 5, 2018, p.052402-1–052402-3.
Imai, M. et al., Angular Momentum Compensation Manipulation to Room Temperature of the Ferrimagnet Ho3-xDyxFe5O12 Detected by the Barnett Effect, Applied Physics Letters, vol.114, issue 16, 2019, p.162402-1–162402-4.

 |