9-3 Theoretical Prediction of “Fermi Arc”

-Development of Novel Method for Analyzing Strongly Correlated Electrons in Heavy-Element Compounds-

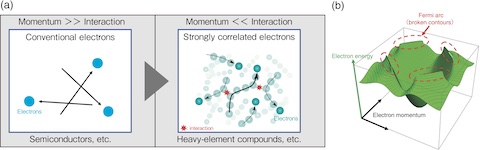
{% pic_name_e_alt %}

This Picture(85kB)

Fig.9-6  Simple descriptions of strongly correlated electrons

Methods for analyzing weakly correlated electrons were well established in the 20th century (Fig.9-6(a), left: blue circles are electrons) semiconductors, etc. It is hard to analyze strongly correlated electrons in heavy-element compounds (Fig.9-6(a), right: light blue circles indicate electrons, red indicates interactions). By extending the equations of quantum mechanics and allowing imaginary numbers to appear in the coefficients of the equations, the complex motion can be accurately captured. As a result, we can theoretically predict the appearance of a “Fermi arc” in the energy behavior of electrons (Fig.9-6(b)).

 

Many of the properties of matter can be explained by the behavior of electrons in matter. Electrons sometimes exhibit strange behaviors. For example, superconductivity, in which electrical resistance suddenly drops to zero, is one such example. By calculating the motion of electrons using quantum mechanics, it is possible to theoretically predict such phenomena. By taking advantage of these properties, various innovative technologies have been developed, such as maglev and MRI technology. The electrons in the copper oxide high-temperature superconductor interact strongly with each other. However, due to these strongly correlated electrons, the phenomenon cannot be reproduced by the conventional calculation method (Fig.9-6(a)). Such materials with strongly correlated electrons are not only high-temperature superconductors but also heavy-element compounds.

Good theoretical ways to analyze strongly correlated electrons might discover unknown materials that exhibit superior properties such as high-temperature superconductivity. Researchers around the world have been developing new computational methods.

In this study, we studied the behavior of strongly correlated electrons in heavy-element compounds. We focused on the fact that there are two kinds of electrons in heavy-element compounds, weakly and strongly correlated electrons. We succeeded in capturing the motion of electrons by using a different quantum mechanical method. As a result, we can theoretically predict a unique phenomenon (a quantum phenomenon called “Fermi arc”) that has not been found in heavy-element compounds. (Fig.9-6(b)).

The Fermi arc is a region where the contour line representing the electron energy level appears to be broken. Fermi arcs have been observed in copper oxide high-temperature superconductors by angle-resolved photoemission spectroscopy, but have not been found in heavy-element compounds. Contour lines are represented as continuous lines, but by extending equations of quantum mechanics and allowing imaginary numbers to appear in the coefficients of the equations, such shredded regions appear.

We might discover novel innovative materials with the use of the developed theory in the future.

This work is partially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (No.JP15K00178, JP18K03552, JP18H04228, and JP16H00995).

(Yuki Nagai)

Reference
Nagai, Y. et al., DMFT Reveals the Non-Hermitian Topology and Fermi Arcs in Heavy-Fermion Systems, Physical Review Letters, vol.125, issue 22, 2020, 227204, 7p.

 |