6-5 New Data Conversion Method to Accelerate Nuclear Simulation

－Matrix Solvers with 16-Bit Operations Achieve Same Convergence as 64-Bit Operations－

Fig.1 Comparison of matrix data conversion methods

Fig.1 Comparison of matrix data conversion methods

The figure shows an example of approximating five-digit matrix data given by the one-dimensional (1D) Poisson equation with an accuracy of four digits. The original matrix satisfies a diagonal dominance condition, in which the absolute value of the diagonal component is greater than or equal to the sum of the absolute values of the nondiagonal components in each row. When approximated by the standard round-nearest data conversion, the diagonal dominance condition is violated. In contrast, the new diagonal-dominant data conversion method preserves the diagonal dominance condition.

 

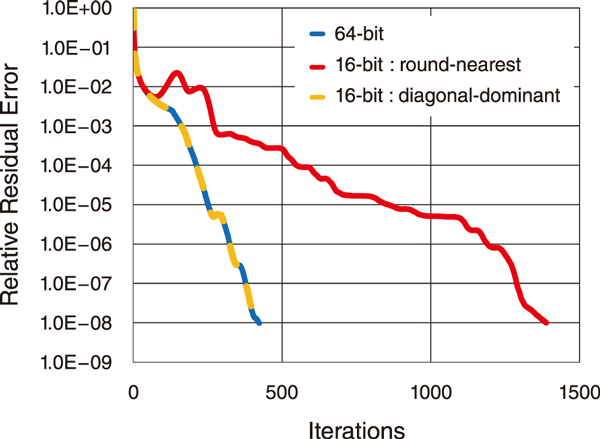
Fig.2 Convergence histories for iterative solvers with Jacobi preconditioners

Fig.2 Convergence histories for iterative solvers with Jacobi preconditioners

The histories of the relative residual error ||b-Ax||/||b|| in iterative solvers for the linear system Ax = b, which is given by Poisson equation on 300 × 300 × 300 grids, are shown. The conversion of 64-bit data to 16-bit data by the round-nearest data conversion increases the number of iterations until the solution converges. However, the diagonal-dominant data conversion produces a solution within the same number of iterations as the 64-bit data.

 

Scientific computation uses 64-bit data, which can represent numbers with approximately 16 digits (the mantissa part). However, with the rise of machine learning, which makes extensive use of 16-bit data to represent numbers of approximately four digits, using 16-bit operations has become important. In particular, the performance of 16-bit operations on state-of-the-art supercomputers is much higher than 64-bit operations. However, it is difficult to obtain reliable results using only 16-bit operations when solving large linear systems commonly encountered in scientific and engineering calculations. Therefore, mixed-precision matrix solvers have been developed to maintain computational accuracy and increase speed by combining 64- and 16-bit operations. In such solvers, data conversion from 64-bit data into 16-bit data is essential, but the rounding error (Fig.1) caused by the difference in the number of representable digits often leads to an increase in the calculation time or the breakdown of the solver.

In this study, a mixed-precision matrix solver based on a new data conversion approach was developed for large linear systems given by Poisson equation; such systems are common in thermal-hydraulic analyses in nuclear reactors. Such large linear systems are usually computed by iterative solvers, in which the convergence properties can be improved by preprocessing approximate solutions and processing the main iterative solvers. Since arbitrary precision can be applied to preprocessing of the approximate solutions, this part can be accelerated by applying 16-bit operations. The Jacobi method, a typical preprocessing algorithm, was used in this study. However, the Jacobi method does not guarantee convergence unless the matrix data satisfies the diagonal dominance condition (Fig.1). When the matrix data are converted to 16-bit data by standard round-nearest data conversion (rounding off), the diagonal dominance condition is violated because of rounding errors, worsening the convergence characteristics and increasing the number of iterations by a factor of three (Fig.2).

In this study, we developed a diagonal-dominant data conversion that rounds diagonal elements toward larger absolute values and nondiagonal elements toward zero to maintain the diagonal dominance condition (Fig.1). The developed method reduced the computation time by approximately 10% while maintaining the same convergence characteristics as 64-bit operations (Fig.2), even when the preprocessing was performed with 16-bit operations.

This result was selected as the Best Paper Finalist at the HPC Asia 2023 International Conference.

This research was partly supported by JSPS KAKENHI Grant-in-Aid for Scientific Research (C) (JP22K12053).

(Takuya Ina)

Reference
Ina, T. et al., A New Data Conversion Method for Mixed Precision Krylov Solvers with FP16/BF16 Jacobi Preconditioners, Proceedings of the International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia 2023), Singapore, 2023, p.29-34.

 |