6-5 原子力シミュレーションを加速するデータ変換手法の開発

−16bit演算を用いた行列解法で64bit演算と同等の収束特性を達成−

図1　行列データの変換方法の比較

1次元ポアソン方程式が与える5桁の行列データを4桁の精度で近似する例を示します。元の行列は各行で対角成分の絶対値が非対角成分の絶対値の和より大きくなる、あるいは、等しくなる対角優位条件が満たされます。標準的な最近接丸め（四捨五入）で近似すると2、3行目で前者が後者より小さくなり、対角優位条件が破れます。一方、新しい対角優位データ変換では対角成分と非対角成分で異なる数値丸め方向を選択し、対角優位条件を維持します。

 

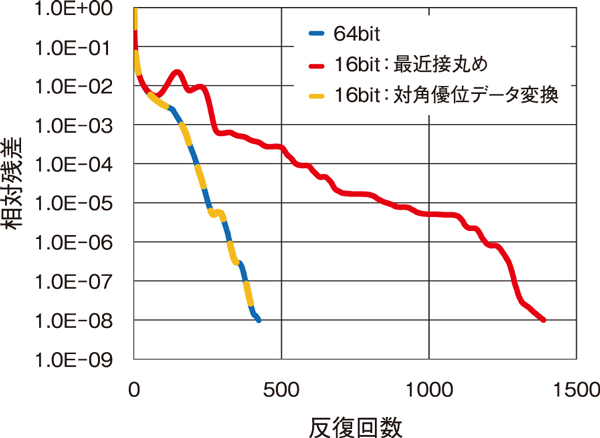
図2　ヤコビ法前処理付き反復解法の収束履歴

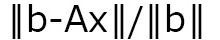300×300×300格子を用いたポアソン方程式が与える連立一次方程式Ax = bの反復解法における相対残差の履歴を示します。64bitデータを最近接丸めで16bitデータに変換すると連立一次方程式の解が収束するまでの反復回数が増加していますが、対角優位データ変換では64bitデータと同じ反復回数で解が得られています。

 

科学技術計算では約16桁の数値（仮数部）を表現可能な64bitデータが利用されます。一方、約4桁の数値を表現する16bitデータが多用される機械学習の興隆により、最先端スーパーコンピュータでは16bit演算の性能が64bit演算の数倍から数十倍に達しており、16bit演算を活用することが重要となっています。しかしながら、科学技術計算で頻繁に計算される大規模な連立一次方程式を解く際には16bit演算のみで信頼できる結果を得ることは困難です。このため、64bit演算と16bit演算を組み合わせて計算精度の維持と高速化を両立する混合精度行列解法の開発が進められています。混合精度行列解法では64bitデータから16bitデータに変換する処理が不可欠ですが、表現可能な桁数の差によって発生する丸め誤差（図1）の影響により計算時間が増加する、あるいは、問題によっては解法が破綻するといった課題がありました。

本研究では原子炉内の熱流動解析に現れるポアソン方程式が与える大規模な連立一次方程式に対して新たなデータ変換手法に基づく混合精度行列解法を開発しました。このような大規模な連立一次方程式は通常、反復解法によって計算されますが、前処理によって近似解を計算してから反復解法を処理することで収束特性を改善できます。ここで、近似解の計算には任意の精度を適用できるため、この部分に16bit演算を適用して処理を加速します。本研究では前処理の代表的なアルゴリズムであるヤコビ法を採用していますが、ヤコビ法は行列データが対角優位条件（図1）を満たさないと収束が保証されないことが知られています。ところが、標準的な最近接丸め（四捨五入）によって行列データを16bitデータに変換すると、丸め誤差によって対角優位条件が破れて収束特性が悪化し、反復回数が約3倍に増大しました（図2）。

本研究では、対角優位条件を維持するために対角要素を絶対値が大きくなる方向に丸め、非対角要素をゼロ方向に丸める対角優位データ変換を開発しました（図1）。開発した手法により、前処理を16bit演算で処理しても64bit演算と同等な収束特性（図2）を維持しつつ計算時間を約10%削減することに成功しました。本成果はHPC Asia 2023国際会議におけるBest Paper Finalistに選定されました。

本研究の一部は、日本学術振興会科学研究費基盤研究（C）（JP22K12053）「ハイブリッド混合精度処理によるエクサスケール反復解法ライブラリの開発」の支援の下で得られた成果です。

（伊奈 拓也）

＜前へ：6-4｜次へ：7 核不拡散・核セキュリティ技術開発＞