図2-12 電磁界方程式の厳密解を得るための計算概念 磁束はデリクレ条件、磁束密度はノイマン条件を与えます。この二つの条件を同時に満たす面をコーシー条件面といいます。

図2-13 JT-60トカマクの4種類のプラズマ電流分布をテストケースとして与えた場合の厳密なテスト形状（青線）と新しい方法による同定形状（赤線）を比較して示します。電流分布のいかんにかかわらず外部の磁束及び磁束密度計測のみで精度の良い磁気面を同定できています。

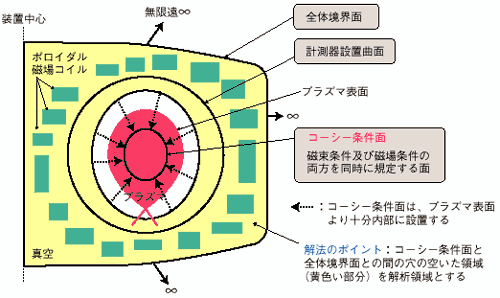
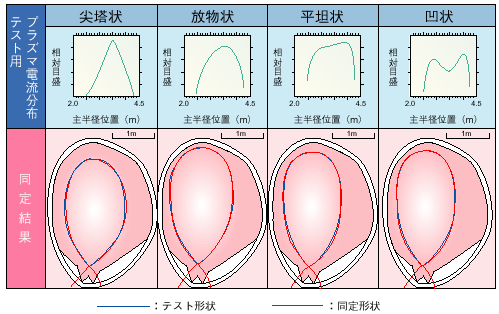
プラズマは荷電粒子の集合体で電磁界を有します。この電磁界からプラズマの断面形状を診断します。電磁界を求めるのには偏微分方程式系（内部を吟味する）で変数分離、あるいは重み関数やグリーン関数を用いる有限要素法と境界積分方程式系（外からためつすがめつする）を用いる方法があります。前者の解を得るためには必要情報量が多岐にわたり、すべてを実測することは現実的でなく、また近似解では診断精度が低下します。後者はプラズマの外側の電磁気量のみで原理的には解を得ますが、積分の収束性が悪い場合には解は不定となり、あるいは不要の解が複数発生する等の不都合がありました。そのため、できるだけ少ない周辺電磁気計測量からできるだけ正確なプラズマ断面形状を同定する新しい方法を考案しました。つまり電磁界の磁束と磁束密度が普遍的に満たす関係が成立する仮想面（コーシー条件面）をプラズマ内部領域につくり、この量を境界積分方程式系に組み込むと速やかにしかも、これまでの方法で得られなかった電流分布においても解を得ます。図2-12に診断法の概念を、図2-13には同定結果の様子を示すことができます｡

参考文献 K. Kurihara, A New Shape Reproduction Method Based on the Cauchy-Condition Surface for Real-Time Tokamak Reactor Control, Fusion Eng. Des., 51-52, 1049 (2000).

ご覧になりたいトピックは左側の目次よりお選び下さい。