図7-1 磁性体R2Fe14Bの結晶構造 黄色い球はNdなどの希土類元素（R）、赤い小さな球はホウ素（B）、青い球は鉄元素（Fe）を表します。

図7-2 磁性体R2Fe14Bの電子密度分布 赤い部分に向かって電子密度が増加しています。図中の記号R（4f）およびR（4g）は希土類、Bはホウ素、Feは鉄元素を表します。

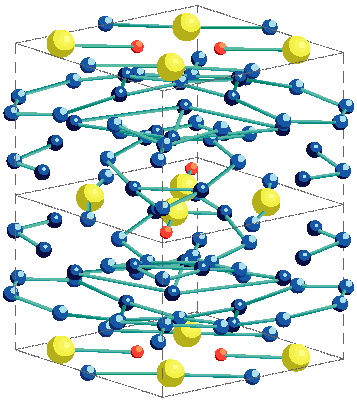
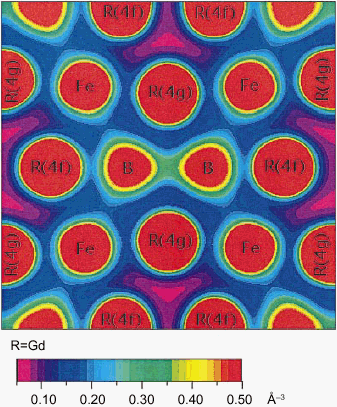
強い永久磁石で代表される磁性体は現代の科学技術を支える重要な材料です。永久磁石は特定の方向に磁化しやすいこと（強い磁気異方性）が必要ですが、主成分である鉄（Fe）等の遷移金属の磁気異方性は余り強くないのでネオジム（Nd）等の希土類元素（R）を混ぜて異方性を強化します（図7-1）。 　物質中の電子分布を表すAlmというパラメータの値を正確に知ることが磁気異方性の強い高性能の磁性体を設計することにつながりますが、実験的にはこの値を高い精度で決定することは大変です。理論的には、量子力学的な計算で電子分布を正確に求めることが基本ですが、膨大な計算時間が必要なため今まで試みられませんでした。私たちは、FLAPW法（線形化補強平面波法）により、希土類・遷移金属・ホウ素化合物（R2Fe14B）の正確な電子分布を計算上の都合からRがガドリニウム（Gd）の場合で計算し、実験的に得られているAlmの値との間に良い一致を確認しました。この方法は結晶内を2つの領域に分けて計算する方法で高精度解析法として定評があります。さらに、このような磁性体における電子密度分布を図示し（図7-2）、強い磁気異方性の発生するメカニズムを視覚的に理解する道を開きました。 　この計算には、ベクトル並列計算機VPPを使って1ケース当たり数週間、全体では1年もかける必要がありました。このように長時間の計算時間を必要とする方法は、現在、必ずしも実用的ではありませんが、上に見たようにこの種の計算が高い精度で実験データを予測できることを考えると、将来の高速計算機で必ず行われる「計算機による物質設計」の先駆けとして大きな意味を持っています。

参考文献 M. Yamaguchi et al., Calculations of the Magnetic Properties of Y2Fe14B and Gd2Fe14X (X=-, B, C, N) by the Full-Potential Linearized Augmented Plane Wave Method, Phys., B, 254, 73 (1998).

ご覧になりたいトピックは左側の目次よりお選び下さい。