図7-5　 キャビティフロー問題。矩形容器に流体を満たし、上端の境界に沿った流れを境界条件として与えて流体の運動を計算します。流体の回転する様子がCA法でも再現できます。

図7-6　 二相に分離した状態からのキャビティフローの時間発展 二相の大きな固まりの中に多数の細かい混じりあいが生じてきます。

図7-7　 キャビティフローの定常状態での界面積濃度の速度・密度依存性 横軸は矩形容器の上端の境界条件として与えられた速度、縦軸は速度=0のところが1になるように規格化した界面積濃度です。

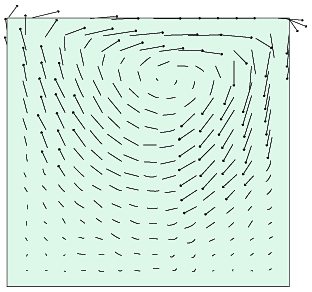
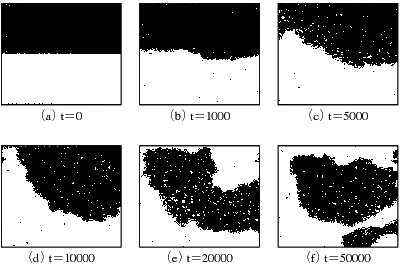
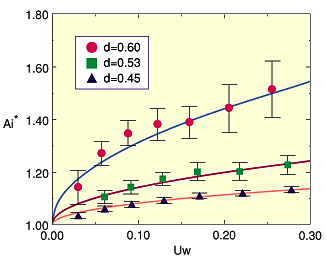
原子炉の冷却水パイプ中に泡が発生して水と蒸気の二つの状態（相）が混在するような時の安全性解析のためには「二相流」のシミュレーションをすることが必要になります。このように溶けあわない二種類の相が混ざっている時には、混じりあえば混じりあうほど二種類の相の境界面が極端に増えてしまい、偏微分方程式に基づくシミュレーションでその振る舞いを知るのはなかなか困難です。この境界面の大きさの尺度は単位体積中に占める境界面の面積、すなわち「界面積濃度」として定義することが出来ます。二つの相の間のエネルギーや物質の移動は境界面を通じて起こるので、界面積濃度がわかれば種々の物理量の二相間の移動が計算できるようになり安全性解析のためのマクロなシミュレーションをすることが出来ます。 　界面積濃度を求めるのに普通の偏微分方程式の求解法に頼れないので従来は実験から求めた相関式に頼ってきました。私たちは、セルオートマトン（CA）法と呼ばれる一種の粒子シミュレーション法を用いて界面積濃度が計算できることを示しました。矩形の容器に流体を満たし上端の境界に沿って流体を動かすような境界条件を与えて流体の挙動を計算する「キャビティフロー問題」（図7-5）について、相分離した状態から出発して二相の混じりあいが起こる様子をシミュレーションしました（図7-6）。十分時間が経つと二相の大きな固まりができてその中に多くの混じりあいが起こるようになります。このシミュレーション結果に対して界面積濃度の速度、密度依存性を求めたものが図7-7です。

参考文献 T. Watanabe et al., Numerical Evaluation of Interfacial Area Concentration Using the Immiscible Lattice Gas, Nucl. Eng. Des., 188, 111 (1999).

ご覧になりたいトピックは左側の目次よりお選び下さい。