10-4 Understanding Fluid Motion in a Spent Fuel Pool

－Proposal of Fluid Analysis Model including Turbulent Effect near Surfaces and Walls of Pool－

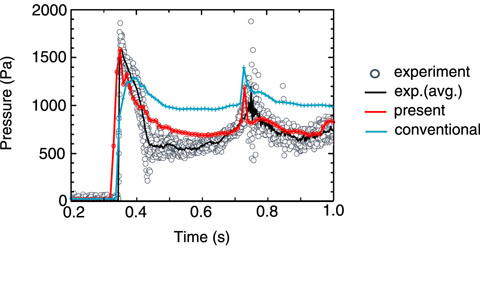
Fig.10-6　Difference in fluid pressure on the wall of a pool between two turbulence models

This Picture(108KB)

Fig.10-6　Difference in fluid pressure on the wall of a pool between two turbulence models

Fluid pressures on the wall of a pool predicted by our model and a conventional model are compared with that measured in an experiment. The predictions of our model are in good agreement with the experimental results.

At a nuclear power facility, spent fuel from the reactor is temporarily stored in a pool of water called spent fuel pool. During an earthquake, the water surface in the pool will undergo dynamic and complex deformation (i.e., sloshing is induced). This sloshing may lead to the overflow of the radioactive water and damage to the pool and the structure attached to the pool by increasing the fluid pressure. To preclude such an occurrence, it is important to know the wave height and fluid pressure resulting from sloshing.

Experiments and conventional numerical simulation studies on sloshing have shown that the wave height is damped by the drag produced by the structure and that the pressure has its maximum value near the water surface. However, the effects of turbulence on the wave height and pressure are not fully understood when sloshing is sustained for a long time, which leads to a transition from laminar to turbulent flow. Hence, in the presence of sloshing and turbulent flow, only conservative estimates have been possible so far.

We propose a turbulence model that can accurately determine all the six components of Reynolds stress to allow estimation in a more qualitative manner and to elucidate the physical mechanism of the turbulence effects. In experiments, it is not easy to investigate each component separately, and simulation is more effective for elucidating the mechanism. However, conventional models do not reproduce experimental results. We found that while its accuracy is insufficient when turbulent eddies transform flat near water surfaces and walls, its accuracy is sufficient for isotropic turbulence. We thought that this inaccuracy could be attributed to the fact that the conventional models only determine three components of Reynolds stress.

Numerical simulation results obtained by using the proposed model with all six components are in good agreement with experimental results, as shown in Fig.10-6. Specifically, the calculated pressure values, such as those corresponding to the two pressure peaks and the relaxation process between the peaks, approximate the experimentally determined values well. Furthermore, the predicted wave height also agrees with the experimental value.

In a future work, we intend testing the model by using it for predicting fluid motion during an earthquake; we shall input actual measured seismic waves.

Reference
Uzawa, K. et al., Effects of Turbulence near a Free Surface on the Dynamics of Two-Phase Flow, Proceedings of 19th International Conference on Nuclear Engineering (ICONE 19), Chiba, Japan, 2011, ICONE19-43453, 8p., in CD-ROM.

 |