2-2 Exploring Latent Uncertainties and Influential Factors in Severe Accident Analysis

－Development of an Integrated Approach to Uncertainty and Sensitivity Analyses for Source Terms－

Fig.2-5 Proposed approach to uncertainty and sensitivity analyses for severe accident source terms

This Picture(62KB)

Fig.2-5　Proposed approach to uncertainty and sensitivity analyses for severe accident source terms

The proposed approach comprises four steps: I. Select the input factors that considerably affect the evaluation of source terms; II. Randomly sample the inputs based on presumed distributions; III. Iteratively execute the SA code until the uncertainty distribution becomes stable; IV. Perform a sensitivity analysis to rank the importance of the inputs. A surrogate statistical model is employed instead of the SA code to avoid unaffordable computational cost during the sensitivity analysis.

 

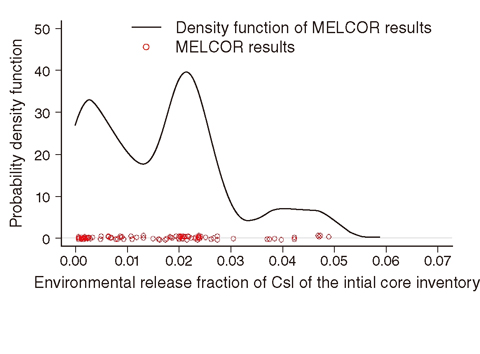
Fig.2-6 Uncertainty distribution of environmental CsI release estimated using MELCOR

Fig.2-6　Uncertainty distribution of environmental CsI release estimated using MELCOR

Based on the 90 runs of the MELCOR code with uncertain inputs relating to fuel cladding failure, collapse of fuel rods, and radionuclide-scrubbing in the water pool, an uncertainty distribution of environmental CsI release is obtained. Although the three inputs are assumed to have uniform or normal distributions, the probability of the output shows a complicated multi-modal distribution.

 

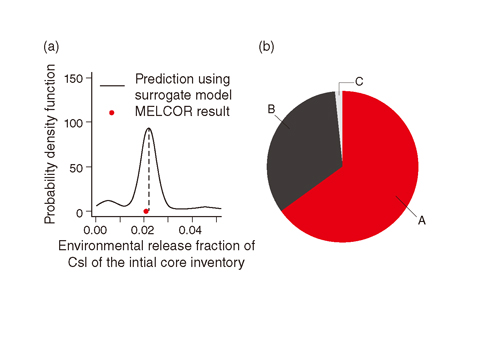
Fig.2-7 Cross-validation of the surrogate model and results of the sensitivity analysis

Fig.2-7　Cross-validation of the surrogate model and results of the sensitivity analysis

(a) The result of MELCOR simulation is in good agreement with the prediction using the surrogate model, whose highest-density interval perfectly contains the actual result. (b) Based on the calculation of the sensitivity indices with the surrogate model, the influence of uncertain inputs associated with fuel cladding failure (A), the collapse of fuel rods (B), and the radionuclide scrubbing in the water pool (C) on output is quantitatively estimated.

Severe accidents (SAs), such as the accident at the TEPCO’s Fukushima Daiichi NPS, involve many complicated physical and chemical phenomena. In general, integrated computer codes with the models for the phenomena are applied to simulate the progression of an SA. The results, however, include uncertainties mainly due to incomplete understanding of these phenomena. To enhance the reliability of simulation results and improve SA analysis codes, evaluation of latent output uncertainties by uncertainty analyses and identification of dominant input factors by sensitivity analyses are necessary.

A novel integrated approach is illustrated in Fig.2-5. Based on the four steps, the uncertainties of the output and influential inputs can be estimated. As an example, MELCOR, an integrated SA code being developed in the United States, is applied to compute the uncertainties for the estimation of the source term (i.e., the amount and timing of environmental radioactive materials release). Fig.2-6 describes the uncertainty of source-term estimation. The environmental cesium iodide (CsI)-release fraction of the initial core inventory is almost in the range between 0 and 0.06, suggesting that the outputs should have this degree of uncertainty in the source term analyses.

To avoid the unaffordable computational cost required for the sensitivity analyses, a surrogate statistical model is constructed using statistical methods whose results can perfectly regenerate the complicated uncertainty distribution shown in Fig.2-6. The results of the sensitivity analysis after the executions of 16000 runs of the surrogate model and the cross-validation of the model are shown in Fig.2-7. Based on the results of the sensitivity analysis, it is clarified that fuel cladding failure had the greatest influence upon the output uncertainty of all the parameters tested.

The above analysis results have confirmed the applicability of the proposed approach to source term analysis during an SA. Hereafter, THALES2, an integrated SA code developed at JAEA with the advantages of simulating the chemical reactions of iodine and the capability of considering various iodine chemical forms other than CsI, will be applied to various SA scenarios for further source term uncertainty analysis. It is foreseen that the latent uncertainty could be discovered and then reduced according to the sensitivity analysis.

Reference
Zheng, X. et al., Application of Bayesian Nonparametric Models to the Uncertainty and Sensitivity Analysis of Source Term in a BWR Severe Accident, Reliability Engineering & System Safety, vol.138, 2015, p.253-262.

 |