10-2　Determination of the Thermal Properties of Nuclear Fuels through Numerical Simulation

－First-Principles Calculations of the Heat Capacity of Plutonium Dioxide－

Fig.10-4 Origins of heat capacity of plutonium dioxide

Fig.10-4 Origins of heat capacity of plutonium dioxide

The left panel shows the crystal structure of plutonium dioxide, where blue and red spheres denote plutonium and oxygen atoms, respectively. The distribution of electronic excitation energies is shown in the bottom-right panel. Heat capacity results from conversion of external heat into atomic-vibrational (lattice-vibrational) and electronic-excitation energies.

 

Fig.10-5 Calculated heat capacity of plutonium dioxide

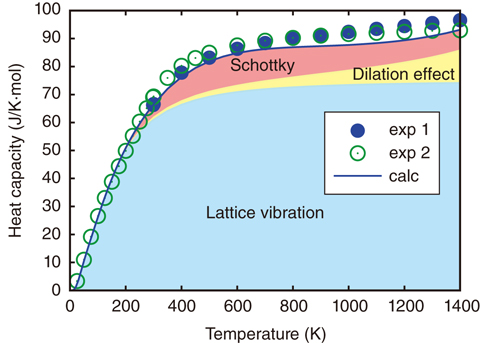
Fig.10-5 Calculated heat capacity of plutonium dioxide

Solid curves represent the calculated results of the heat capacity of PuO2, and circles correspond to experimental data. The calculated lattice heat capacity, dilation effects, and Schottky heat capacity are illustrated separately. The calculated result agrees well with the experimental data.

 

To improve safety, it is important to have adequate knowledge of the thermal properties of nuclear fuel. However, it is difficult to accurately measure these properties at high temperature in experiments. Thus, numerical simulations are expected to compensate for insufficient experimental data. In nuclear-fuel development, one important thermal property is heat capacity, which corresponds to the heat needed to raise the temperature of the material a unit of temperature. So far, numerous theoretical and experimental studies have been conducted on precise measurements of the heat capacity of nuclear fuel and on understanding the mechanism giving rise to this capacity. One of the problems found in these studies is that the theoretically predicted heat capacity does not agree with measurements in the case of plutonium dioxide (PuO2), which is one of main ingredients of nuclear fuel.

To solve this problem, we aimed to reproduce the heat capacity of PuO2 using numerical simulation based on first-principles calculation, which is a reliable method for calculating the properties of materials based purely on interactions between nuclei and electrons, without the requirement for any empirical parameters. First, we evaluated the lattice heat capacity (Fig.10-4) as lattice vibration was expected to be the main source of the heat capacity in this material. The calculated lattice heat capacity was, however, not sufficient to reproduce the observed total heat capacity. Second, we tried to evaluate so-called Schottky heat capacity owing to electronic excitations. In PuO2, some electrons bound in Pu atoms jump up to high-energy excited states at high temperatures; thus, the electronic excitation affects the heat capacity. So far, Schottky heat capacity has been evaluated with simple models considering only a few excited states, but these results have not agreed with experimental data. In contrast, we adopted more than 100 excited states obtained by first-principles calculations and recalculated the Schottky heat capacity. We then succeeded in reproducing the total heat capacity, as shown in Fig.10-5. This precise evaluation could not have been attained without first-principles calculations.

In this study, we succeeded in accurately evaluating the heat capacities of nuclear fuel materials by numerical simulation based on first-principles calculation. However, other thermal properties such as thermal conductivity are required to develop safer fuels. Thus, we will challenge accurate predictions of other nuclear-fuel properties by first-principles simulations and would like to contribute to the development of secure nuclear fuels.

Reference
Nakamura, H. et al., First-Principles Calculation of Phonon and Schottky Heat Capacities of Plutonium Dioxide, Journal of the Physical Society of Japan, vol.84, no.5, 2015, p.053602-1-053602-5.

 |