4-3　Computational Design of High-Toughness Alloys

－Magnesium-Alloy Design from Electronic-Structure Calculations－

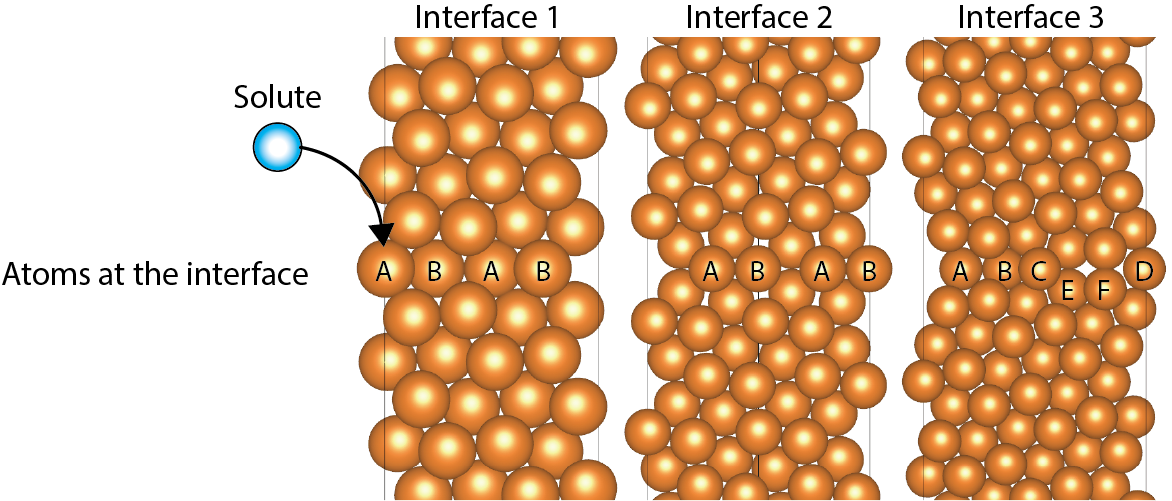
Fig.4-6 Atomic models of the interfaces

Fig.4-6 Atomic models of the interfaces

Relaxed atomic configurations of the (1) (1011), (2) (1012), and (3) (3032) TBs in pure Mg. Possible segregation sites used in the DFT calculations are shown by A to F in each interface.

 

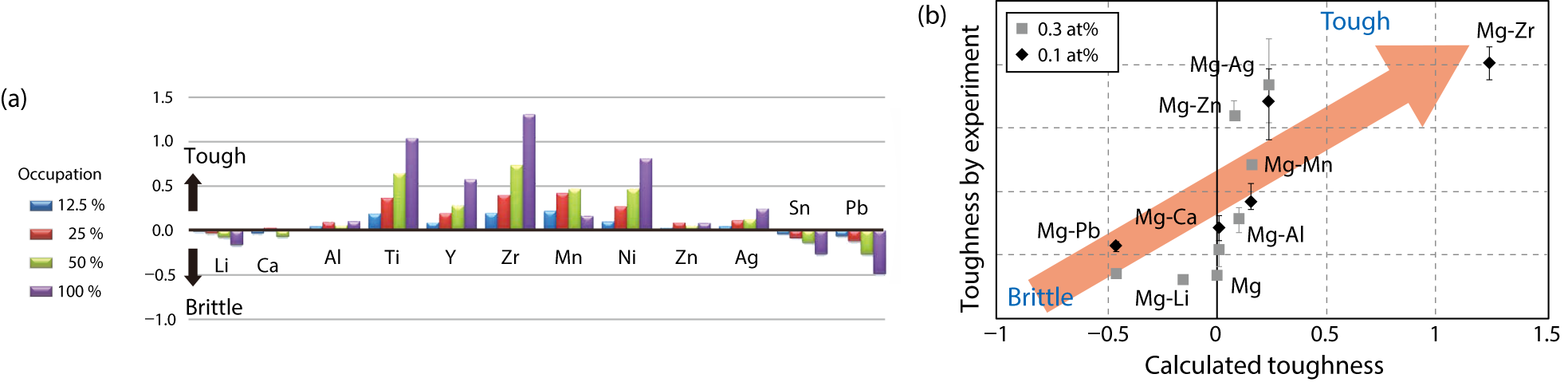
Fig.4-7 (a) Ideal work of interfacial-separation in terms of site occupation (12.5%?100%). (b) Fracture-toughness relationships between experiments and simulations

This Picture(161kB)

Fig.4-7 (a) Ideal work of interfacial-separation in terms of site occupation (12.5 %–100 %). (b) Fracture-toughness relationships between experiments and simulations

We investigated the effect of alloying elements on the toughness with respect to the occupation. The negative and positive values correspond to weakening and strengthening effect, respectively. The calculated values are in good agreement with the experimental ones. Thus, we can predict the potential candidate for alloying elements which improve the toughness.

 

Mg alloys are promising candidates for next-generation lightweight structural materials in terms of energy and environmental conservation, especially for use in transportation equipment. However, widespread application of wrought-Mg alloys is limited by their low formability at room temperature. This low formability is caused by their low ductility and fracture toughness. The former is because of their strong plastic anisotropy originating from their hexagonal close-packed (HCP) structure and the latter is attributed to the intrinsic features of their electronic structure.

An important property for improving formability is fracture toughness, because pure Mg is intrinsically brittle, with local strain concentration occurring at twin boundaries (TBs) and cracks mainly propagating along these boundaries. We have systematically investigated the fracture toughness of Mg-X binary alloys from the viewpoint of the effects of solute elements. In the present study, we introduce an electronic-structure-based approach combined with fracture mechanics to understand the effect of solute elements upon the interfacial fracture of Mg alloys. Rather than solely focusing upon the segregation energy at the surface and interface, we focus on the comprehensive mechanism caused by the electronic structure, which dominates cohesion or decohesion of the interfacial fracture.

Fig.4-6 shows atomic models of typical TBs observed in experiments. We constructed several types of TB configurations to investigate the effects of various solute elements upon the ideal work of interfacial separation. Three different TBs were constructed to investigate differences in the type of boundary, including energetically stable and unstable boundaries. The free-surface energy was evaluated, together with the interfacial energy and the energy-based Griffith criterion for crack propagation was applied.

The difference in the ideal work of interfacial separation between the Mg-M alloys and pure Mg in terms of the occupancy at the TB site for the (1012) TBs is summarized in Fig.4-7(a), with positive values corresponding to solutes with toughness. The values for Li, Ca, Sn, and Pb are very small or negative, indicating that these elements cause segregation-induced embrittlement at the interface. On the other hand, the other solutes show positive values and Zr has the highest among them. Finally, we compare the calculated values with experiments in Fig.4-7(b), where our prediction shows good agreement with the experimental values and the toughness is indeed improved by the Zr solute.

We conclude that the electronic interactions of both the bulk and the surface and their difference characterize the fracture toughness of binary alloys. We hope that computational simulations will play a more important role in the effective approach for new-alloy design.

This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant-in-Aid for Scientific Research (C) (No.16K06714).

Reference
Tsuru, T. et al., Interfacial Segregation and Fracture in Mg-Based Binary Alloys: Experimental and First-Principles Perspective, Acta Materialia, vol.151, issue 1, 2018, p.78–86.

 |