Fig.9-2 Schematic figure of the quantum manybody system calculation (a) and the Monte Carlo method (self-learning Monte Carlo method) using machine learning (b)
Many of the properties of matter are explained by the behavioral differences of the electrons in the material. In particular, materials such as copper oxide high-superconducting-transition-temperature (high-Tc) superconductors and heavy element compounds including uranium etc. are called strongly correlated electron systems in which electrons strongly interact with each other. Understanding of electron behavior in these materials is one of the important problems in modern solid-state physics. In order to accurately simulate the behavior of these electrons, quantum simulation that takes quantum mechanical properties of electrons is necessary. For example, in the superconducting state where the resistance becomes zero, it is known that electrons move in pairs, but in the copper oxide high-temperature superconductor at a high temperature above the liquid nitrogen temperature, the behavior of the electrons has not been fully understood and its superconducting mechanism is one of the big mysteries of solid-state physics. There are many quantum simulation, theoretical analysis, and experiments.
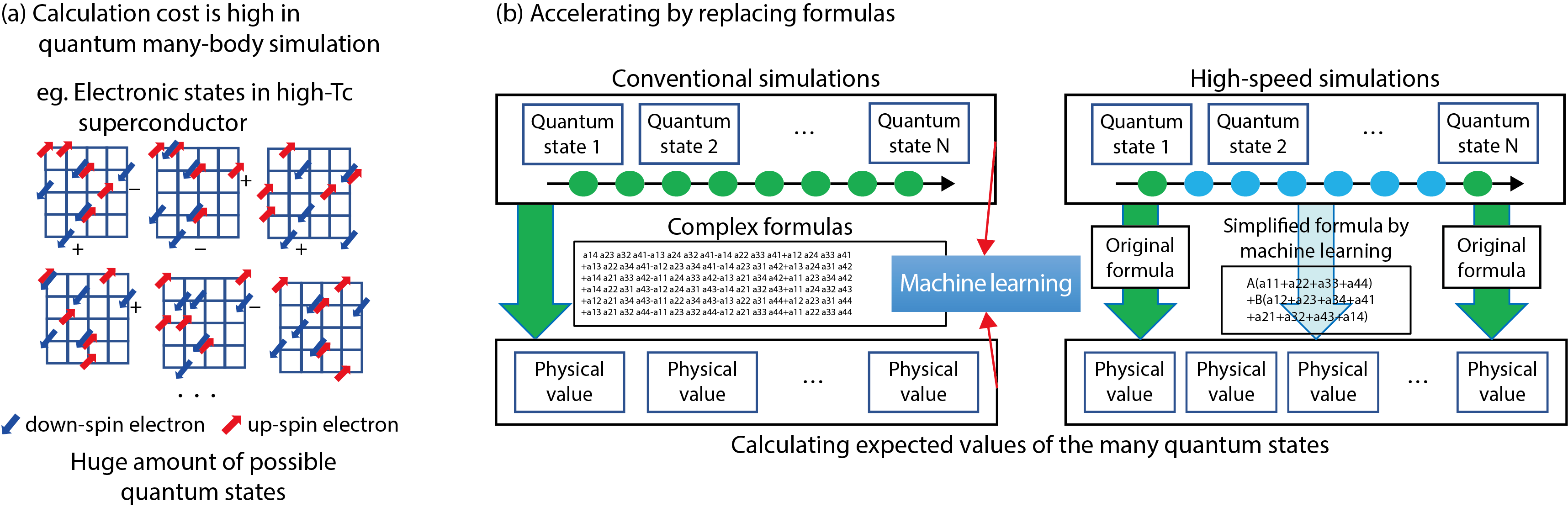
However, in quantum simulation, when the number of electrons increases, the number of electron states that we have to consider increases exponentially. Thus, the calculation cost is very high and even if the latest supercomputer is used. It is difficult to fully understand strongly correlated electron systems (Fig.9-2(a)). Therefore, many researchers all over the world are trying to develop highly accurate and fast calculation methods.
In this research, we focused on “Machine Learning”, which has been developing rapidly in the field of computational science in recent years. From a huge amount of data, machine learning can find patterns are difficult for human beings to find. In this research, we succeeded in developing a faster method (self-learning Monte Carlo method) by creating an effective model by extracting its essence using machine learning in quantum Monte Carlo simulation which is a highly accurate quantum simulation method.
In Markov chain Monte Carlo simulation, we calculate the physical quantity (such as electron density) by using stochastic process called Markov chain made by target model. However, to calculate the transition probability of Markov chain, it is necessary to calculate using a very complicated expression reflecting the complexity of the quantum system. Therefore, we execute traditional simulation as a trial simulation, gather learning data on this complicated calculation formula, and finding out the pattern behind it by machine learning to construct an effective model represented by a simple calculation formula. In this simulation, it is possible to calculate the physical quantity at a high speed (up to 10000 times) by sandwiching the simulation with this effective model (Fig.9-2(b)).
Using this high-speed method, it becomes possible to deal with complicated models reflecting the structure of more realistic substances, and it is expected to elucidate the variety of physical properties of materials which have been a mystery until now.
<Previous: 9 Computational Science and E-Systems Research | Next: 9-2>