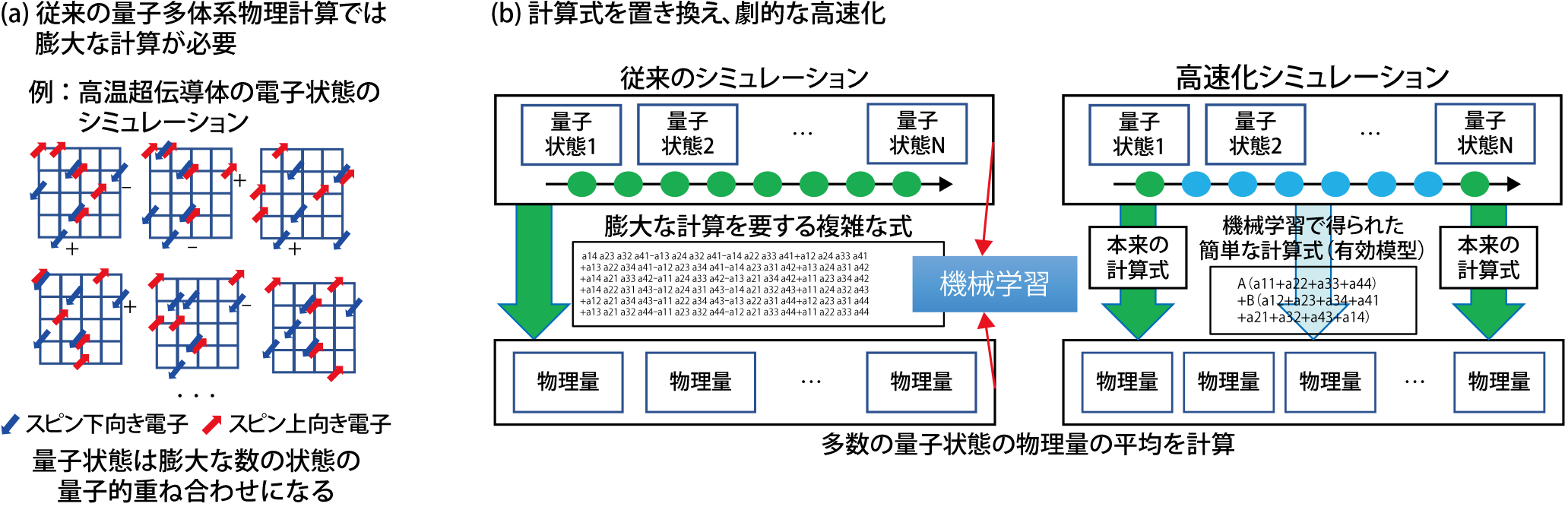
図9-2 計算手法の概略と模式図
物質の性質の多くは、その物質に含まれる電子集団の振る舞いの違いによって説明されます。特に、銅酸化物高温超伝導体やウラン等を含む重元素化合物などの物質は、電子同士が強く相互作用する強相関電子系と呼ばれており、これらの物質での電子の挙動の理解は現代の固体物理学における重要な問題の一つとして位置づけられています。これらの電子集団の振る舞いを正確にシミュレーションするためには、電子の量子力学的性質を考慮した量子シミュレーションが必要です。例えば、電気抵抗がゼロになる超伝導状態においては、電子はペアを組んで運動することが知られていますが、液体窒素温度以上の高温で超伝導体になる銅酸化物高温超伝導体中での電子集団の挙動は分かっておらず、その超伝導メカニズムは固体物理学ひいては物理学全体の大きな謎の一つとなっており、量子シミュレーションや理論解析、実験により盛んに研究が行われています。
しかしながら、量子シミュレーションは、扱う電子の数が増えると考慮しなくてはならない場合の数が指数関数的に増大していくため計算負荷が非常に高く、現在の最新のスーパーコンピュータを用いたとしても強相関電子系を十分に理解することは困難でした(図9-2(a))。そこで、世界中の多くの研究者が高精度で高速な計算手法の開発を試みています。
本研究では、近年計算科学分野で急速に発展している「機械学習」に着目しました。機械学習とは、膨大なデータをコンピュータに学習させることで、その背後にあるパターンなどを自動的に見いだす手法で、人間には見つけ出すことが困難なパターンも見いだすことが時に可能となります。本研究では、高精度な量子シミュレーション手法である量子モンテカルロシミュレーションにおいて、機械学習を用いてその本質を抽出した有効模型を作成し、高速にシミュレーションする手法(自己学習モンテカルロ法)を開発することに成功しました。
マルコフ連鎖モンテカルロシミュレーションでは、対象となる模型が作るマルコフ連鎖という確率過程を用いて物理量(電子密度等)を計算します。しかし、シミュレーションを行うために必要なマルコフ連鎖の遷移確率の計算には、量子系の複雑さを反映した非常に複雑な式を用いた計算が必要となります。そこでトライアルシミュレーションとして従来のシミュレーションを実行しこの複雑な計算式に関する学習データを集め、機械学習によりその背後にあるパターンを見いだすことで簡単な計算式で表される有効模型を構築します。本シミュレーションではこの有効模型でのシミュレーションを途中に挟むことにより、物理量を高速(最大で1万倍)に計算することができます(図9-2(b))。
本研究による高速化によって、より現実の物質の構造を反映させた複雑な模型を取り扱うことが可能となり、これまで謎となっていた物質の多彩な物性の解明が期待されます。