9-2 Matrix Solvers for Multiphase CFD Simulations with One Hundred Billion Grids

－Communication Avoiding Multigrid Methods－

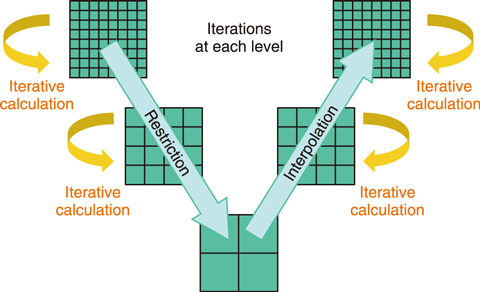
Fig.9-4 Multigrid method

Fig.9-4 Multigrid method

Multigrid methods interpolate solutions on multi-scale grid systems with different resolutions and reduce errors at different scales independently by iterative calculations, leading to improved convergence properties in multi-scale problems.

 

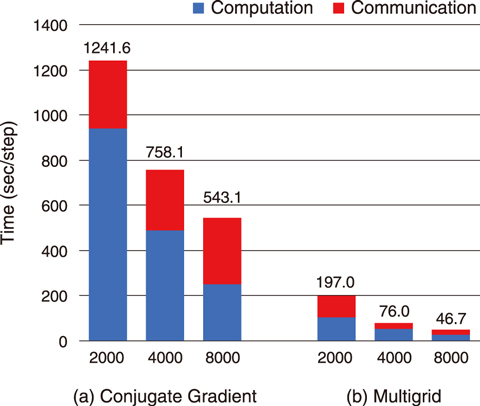
Fig.9-5 Scaling of computational performance up to the full system of the Oakforest-PACS supercomputer

Fig.9-5 Scaling of computational performance up to the full system of the Oakforest-PACS supercomputer

The computational performances of the conventional matrix solver: (a) (i.e., the preconditioned conjugate gradient method) and the proposed matrix solver: (b) (the multigrid preconditioned conjugate gradient method) are shown using the Oakforest-PACS supercomputer in JCAHPC with 8000 computing nodes.

 

JAEA promotes the development of multiphase computational fluid dynamics (CFD) to analyze complex thermal hydraulic phenomena in reactor core including structure materials and molten debris in severe accidents. Future exascale supercomputers are expected to enable whole reactor simulations that require one hundred billion grids. However, such large-scale simulations are characterized by multi-scale phenomena, and pressure Poisson solvers, which are main components in the multiphase CFD codes, show significant convergence degradation. A matrix solver was therefore proposed to compute multi-scale problems efficiently. As a result, an order of magnitude speedup was achieved in multi-phase CFD simulations with one hundred billion grids.

Solutions of multi-scale problems involve errors in the long and short wavelength regimes. Although matrix solvers are converged by reducing errors through iterative calculations, the information propagation of long-wavelength errors takes more time with a larger number of grids, leading to slower convergence. A multigrid method was thus introduced for use in multi-scale problems. In this method, slow convergence is avoided by reducing errors at different scales on multi-scale grid systems independently (Fig.9-4).

Research aimed at reducing the computational and communication costs for iterative calculations at each level was also required. The precision requirement on the multigrid method was first relaxed by using it as a preconditioner for the conventional conjugate gradient (CG) method, and single (32 bit) and double (64 bit) precision computations were then applied to the multigrid and CG methods, respectively. This mixed precision approach enabled a 50% reduction of computation and communication in the multigrid method while maintaining the precision of final solutions. The developed solver was tested in multiphase CFD simulations with one hundred billion grids on the Oakforest-PACS, which is the largest CPU-based supercomputer in Japan; a speedup of 11.6x speedup compared with the conventional matrix solver was achieved (Fig.9-5).

This study was supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan (Grant for Post-K priority issue No.6), “Development of Innovative Clean Energy”, and carried out under the project “Large-scale HPC Challenge”, the Joint Center for Advanced High Performance Computing (JCAHPC).

Reference
Idomura, Y. et al., Communication Avoiding Multigrid Preconditioned Conjugate Gradient Method for Extreme Scale Multiphase CFD Simulations, Proceedings of 9th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2018), Dallas, USA., 2018, p.17−24.

 |