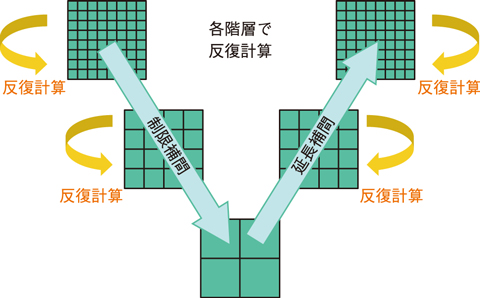
図9-4 マルチグリッド法のアルゴリズム
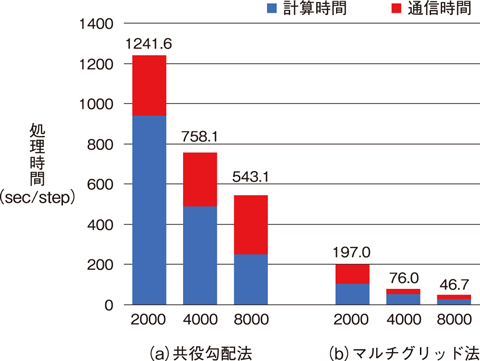
図9-5 Oakforest-PACS全系に至る計算性能のスケーリング
過酷事故時の原子炉内における構造物や溶融物を含む複雑な熱流動現象を解析するために多相流体解析コードが開発されており、将来のエクサスケール計算機では1000億格子規模を必要とする原子炉全体のシミュレーションが可能になると期待されます。しかしながら、このような大規模解析では現象のマルチスケール性が顕著になり、多相流体解析コードの中核を成す圧力方程式の行列ソルバの収束特性が悪化していくことが問題となっていました。今回、このようなマルチスケール問題を効率的に計算できる行列ソルバを開発し、1000億格子規模の多相流体解析を10倍以上高速化することに成功しました。
マルチスケール問題の解には長い波長と短い波長の誤差成分が混在します。行列ソルバでは反復計算によって誤差を減衰させて解を収束させますが、格子数を増やすと長い波長の成分の情報伝播に時間が掛かり誤差の減衰が遅くなります。このため、従来の解法では問題規模に伴って反復回数が増大し、大規模問題の解析が困難でした。この課題を解決するために、マルチグリッド法と呼ばれるマルチスケール問題向けの解法を導入しました。この手法では、格子幅の異なる階層的な格子系において、異なる波長の誤差成分を独立に減衰させるため、反復回数の増大を回避することができます(図9-4)。
一方、計算コストの観点からは、各階層での反復計算の演算量と通信量を削減することが課題となっていました。そこで、本研究では、マルチグリッド法を従来の共役勾配法の近似的前処理として用いることで、マルチグリッド法処理の精度要求を緩和し、マルチグリッド法に単精度計算(32ビット)、共役勾配法に倍精度計算(64ビット)を用いる混合精度計算を適用することで、マルチグリッド法の計算量と通信量を半減しつつ最終的に得られる解の精度を維持することに成功しました。国内最大の汎用CPU型スーパーコンピュータであるOakforest-PACSを用いて1000億格子規模の多相流体解析の性能評価を実施したところ、従来の行列ソルバに比べて約11.6倍の性能向上を達成しました(図9-5)。
本研究は、文部科学省ポスト「京」重点課題⑥「革新的クリーンエネルギーシステムの実用化」及び最先端共同HPC基盤施設「大規模HPCチャレンジ」の支援により得られた成果です。