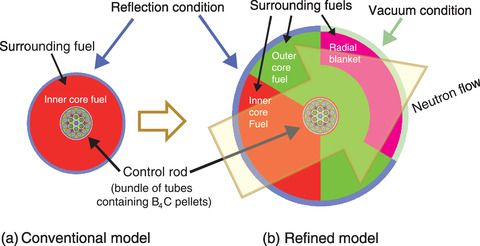
Fig.7-5 (a) Conventional and (b) refined geometric model of the control rod and surrounding fuels
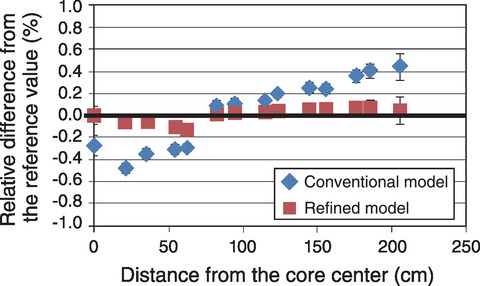
Fig.7-6 Improved radial power distribution for a large core
The control rod is an important device that is used to operate and control a nuclear reactor. Incorrectly estimating the neutron absorption effect of a control rod leads to an improperly designed core. In particular, the radial power distribution in radially flattened large cores is affected by control-rod calculation errors, leading to excessive allowance in core design.
The core design calculation is performed in two steps. In the first step, the detailed structure of core components is focused on individually, such as that of the control rod or fuel assembly. An overall core calculation is then performed in the second step without treating the detailed structure, where the nuclear reaction data are multiplied by a set of coefficients to reproduce the results from the first step. The reaction rate ratio preservation (RRRP) method had been established to calculate the necessary parameters of the control rods in the first step. In this method, the nuclear reaction data are multiplied by the ratio of neutron absorption reaction rate in the control rod to that of the surrounding fuels.
Conventionally, the geometric model of the control rod and surrounding fuels shown in Fig.7-5(a) is used in the first calculation step for all control rods in the core. We reconstructed this model. To evaluate the adequacy of the model, we adopted the ratio of neutron absorption reaction rate of control rod to that of the surrounding fuels (α), which is an essential component of the RRRP method. The proposed model was then verified by the Monte Carlo (MC) method that can simulate an entire core configuration with detailed control rod and fuel structures. An improvement of the conventional deterministic method was still required for core design, since the statistical MC method requires extensive calculation time.
Simple modifications, such as adjusting the number of surrounding fuel assemblies per control rod to meet that of the target core, allowed for clear improvements to the value of α for the control rods near the core center, thereby reducing the calculation error caused by the overestimation of neutron absorption of control rods. However, the value of α for control rods further from the core center did not agree with the reference value, possibly because the control rods were surrounded by plural fuel regions (i.e., inner core fuel, outer core fuel, radial blanket); because neutrons flow from the core center to the core exterior, the neutron flow behavior depends on the direction. We then proposed a refined model, as shown in Fig.7-5(b), to address this problem and improve the overall value of α. The refined model not only simulates the surrounding plural fuel regions with sector dividing but also employs two boundary conditions, reflective and vacuum, to simulate the neutron flow.
Evaluating the resulting core design calculations with several control-rod insertion patterns demonstrated that the proposed refined model significantly improved the calculation accuracy of control-rod worth and radial power distribution. The relative error from the reference value (i.e., using the MC method) decreased below 0.13% (one-sixth of that using the conventional model) for the control-rod reactivity worth, below 0.35% (one-third) for the radial power distribution as an example shown in Fig.7-6. Overall, the proposed control-rod calculation method can be applied to large fast reactor core design with high accuracy.
(Kazuo Takino)