4-9 Progress in Stability Theory for Rotating Plasmas

－New Matching Theory for Resistive Wall Modes－

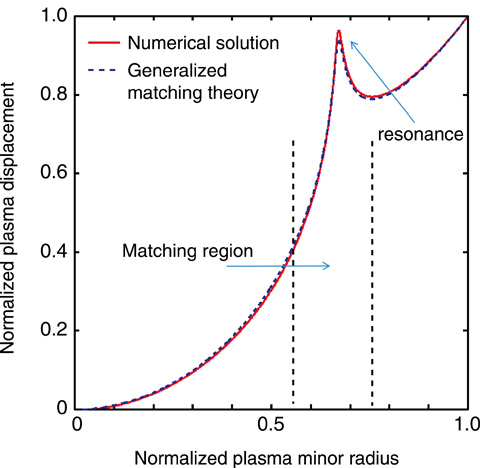
Fig.4-22　Plasma displacement by generalized matching theory

Fig.4-22　Plasma displacement by generalized matching theory

Using a matching region with finite width, the resonant structure of RWM is captured. In matching theory, physical quantities controlling RWM stability can be identified by changing the physical model in the matching region.

 

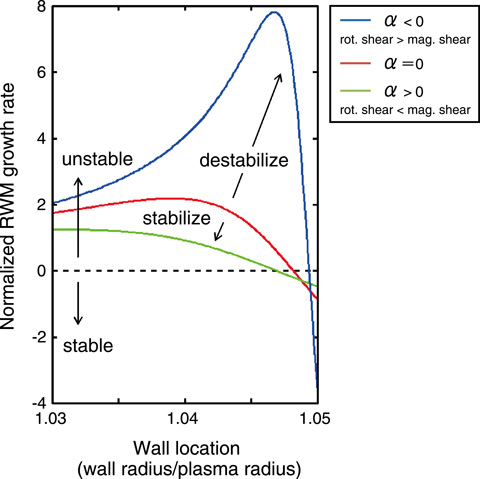
Fig.4-23　RWM stability analysis by analytic dispersion relation

Fig.4-23　RWM stability analysis by analytic dispersion relation

Dependence of RWM growth rates on the wall location is shown by the analytic dispersion relation via generalized matching theory. Here, α denotes a physical parameter that depends on profiles of rotation and magnetic field.

The JT-60SA device that is being constructed in the Naka Fusion Institute aims to realize advanced (high-beta, steady) plasmas to contribute to ITER and DEMO research. In advanced plasmas, one of the most important issues is that the achievable plasma beta value is limited by the occurrence of instability called resistive wall modes (RWMs). It is known that the use of plasma rotation is an effective way to stabilize the RWMs. However, the stabilizing mechanism and the most essential physical quantities (magnetic field, temperature, density, etc.) have not yet been clarified.

In stability analysis, there is a method called “matching theory” that can extract the most essential physical quantity controlling stability. In matching theory, the asymptotic matching method has been established. In this method, the region governed by the most essential physics (physically it appears as a resonance and the region is called the resonant surface) is asymptotically connected to the region that is apart from the resonant surface. Without rotation, the location of resonance is determined by background magnetic field, thus asymptotic matching theory is valid because we know the behavior of the solution around the resonant surface. However, with rotation, the resonant surface splits due to Doppler shift. Furthermore, because the RWM rotates with finite frequency and resonates, the location of resonance shifts away furthermore. The locations of these resonant surfaces are not known a priori, hence, the asymptotic matching theory fails to capture the resonance. To overcome this difficulty, the matching theory is generalized. The generalized matching theory invokes a matching region with finite width to include the resonant surface, because the location of resonance is limited to a finite range. With the aid of the matching region with finite width, we can solve the matching problem for rotating plasmas (Fig.4-22).

Generalization of matching theory enables us to derive an analytic dispersion relation that describes the RWM stability (a relation among the RWM wave number, growth rate, and frequency). By analyzing the dispersion relation, the most influential physical quantity for RWM stability has been clarified. This physical quantity is determined by profiles of plasma rotation and magnetic field. By studying how this physical quantity affects the RWM stability, it is found that when the rotational shear is smaller (larger) than the magnetic one, the rotation stabilizes (destabilizes) the RWM (See Fig.4-23, where the physical quantity is denoted by α). This result is applicable for designing the profiles of rotation and magnetic field that are suitable for stabilizing the RWMs.

Reference
Shiraishi, J. et al., Analytic Dispersion Relation for Resistive Wall Modes in Rotating Plasmas by Generalized Matching Theory, Nuclear Fusion, vol.51, no.5, 2011, p.053006-1-053006-9.

 |