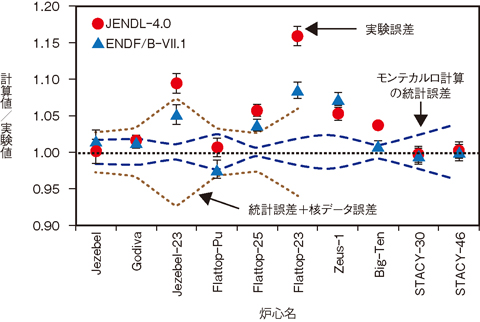
図4-3 計算結果と実験値の比較
表4-1 原子炉動特性パラメータを計算した臨界集合体
炉心解析におけるモンテカルロ法は、中性子の振る舞いを忠実にシミュレーションすることによって、原子炉の核特性パラメータを計算する手法です。この手法は、原子炉設計計算でよく用いられている決定論的手法と比べると、非常に正確に炉心体系を表現することができます。さらに、中性子が原子核と衝突するときの断面積を連続的に取り扱うことができます。すなわち、モンテカルロ法を用いますと、ほとんど近似の入らない高精度の計算が可能となります。
このように大きな利点のあるモンテカルロ法ですが、原子炉の炉心解析で必要となる全ての核特性パラメータを計算することはできません。これまでモンテカルロ法で計算できなかったパラメータの一つが原子炉動特性パラメータ、すなわち実効遅発中性子割合と中性子生成時間です。これらは、原子炉の出力変動に直接関係する核的な安全性パラメータです。これらの値が少し異なるだけで、原子炉出力に対し、指数関数的に影響を及ぼすことになりますので、できるだけ正確に計算したいという要求があります。
私たちは、これらの原子炉動特性パラメータをモンテカルロ法で計算する新しい手法を開発しました。計算が困難であった理由は、これらのパラメータが随伴中性子束で重みづけられた反応率の比で定義されていたからですが、新しい手法では随伴中性子束を用いることなく、実効増倍率の微分係数から厳密に動特性パラメータを計算することができます。新手法を検証するため、私たちが開発しているモンテカルロコードMVPにこの手法を実装し、種々の臨界集合体(表4-1)に対して遅発臨界時のα値を比較しました。図4-3は、その結果を示したものです。遅発臨界時のα値は、実効遅発中性子割合を中性子生成時間で割った値に−1をかけた値として定義され、臨界実験で精度良く測定できる核特性パラメータです。体系によっては大きくずれているものも見られますが、おおむね、モンテカルロ計算の統計誤差と使用した核データの誤差に起因する誤差の範囲内で実験値を再現できることが分かります。
モンテカルロ法で精度良く動特性パラメータを計算できるようになり、燃料デブリ体系や新型炉に対して動特性パラメータの参照解を与えることができると期待されています。