11-4　流体-構造相互作用シミュレーションの高速化

−流動により振動する原子炉機器・配管の挙動解析シミュレーション技術を開発−

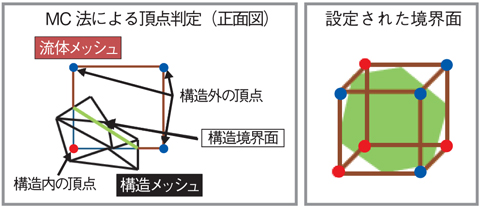
図11-8　MC法を用いた境界面設定手法

流体メッシュの頂点に対し、構造メッシュに含まれる点 （）と含まれない点 （） を判定し、その判定結果から境界面を簡易的に設定します。実際の形状を正確に計算しないため、計算量を大幅に削減できます。

 

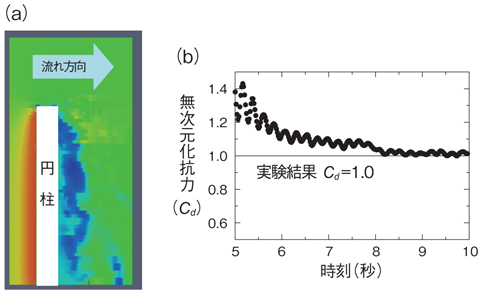
図11-9　円柱周辺の圧力分布図と抗力の時間変化

（a）圧力分布図です。円柱の上流側に高い圧力 （赤） が、下流側に低い圧力 （青） が生じています。（b）（実験結果との比較）より、計算結果が実験値に収束していく様子が分かります。

 

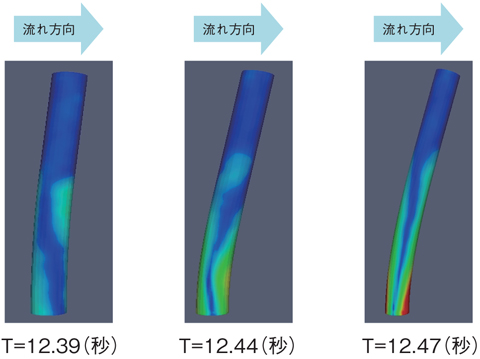
図11-10　円柱形状の時間変化

応力が高い領域を赤、低い領域を青で表示しています。円柱周辺で圧力差が生じた結果、時間と共に円柱が変形する様子が分かります。円柱の変位は100倍に拡大して表示しています。

原子力施設の機器や配管における流動現象（圧力変動，渦，気泡など） に起因した振動 （流動励起振動） は破損やひび割れの要因になることから、原子力施設の安全性にかかわる重要な現象のひとつとなっています。複雑な機器や配管における流動励起振動を詳細に把握するための方法論として、流体，構造，その相互作用をすべて数値シミュレーションで解析する手法 （流体・構造連成シミュレーション） が注目されています。流体・構造連成シミュレーションでは、対象となる流体・構造物が存在する領域を小さな多面体 （メッシュ） で分割して計算する方法が一般的です。

従来は、流体と構造の境界面の形状にメッシュの形状を一致させる手法を用いてきました。この手法は、構造物が複雑に変形した場合、流体メッシュの形状がいびつになるため計算精度の劣化や計算速度の低下を引き起こし、最終的には計算できなくなることがあります。これらの問題の解決策として、流体メッシュを完全な直方体で作成し、構造物の影響は流体メッシュ内における外力として考慮する Immersed Boundary法（IB法）の適用があります。しかし、IB法は境界面をモデル化した場合、境界面の設定に膨大な計算時間を要することが課題でした。

そこで、IB法を適用する際の境界面設定アルゴリズムにCGアルゴリズムのひとつ、マーチングキューブ法（MC法）を組み合わせる手法を考案しました（図11-8）。本手法により、実際の形状を正確に計算する手法と比べて最大で20倍以上の高速化を実現しました。これまで半年かかった計算を10日以内で終えることができるため、より実用的な研究が可能となります。

本手法を円柱の流動励起振動シミュレーションに適用し、精度検証を実施しました。図11-9（a），図11-10に示すように、円柱の影響を受けて周辺の流体領域に圧力差が生じ、その影響で円柱が変形していく様子が伺えます。円柱に対し発生する抗力の大きさ（図11-9（b）） や円柱の変形量などを実験値及び理論値と比較することで、本手法が実問題に適用可能な精度を備えていることを確認しました。

本研究により、高速かつ実問題に適用可能な精度を備えたIB法による流体・構造連成シミュレーションを実現しました。本手法を用いることで、複雑に変形する大規模な流動励起振動シミュレーションが可能となり、原子力施設の安全性を高めるための技術開発に寄与することが期待されます。

＜前へ：11-3 ｜次へ：12 核不拡散科学技術開発 ＞