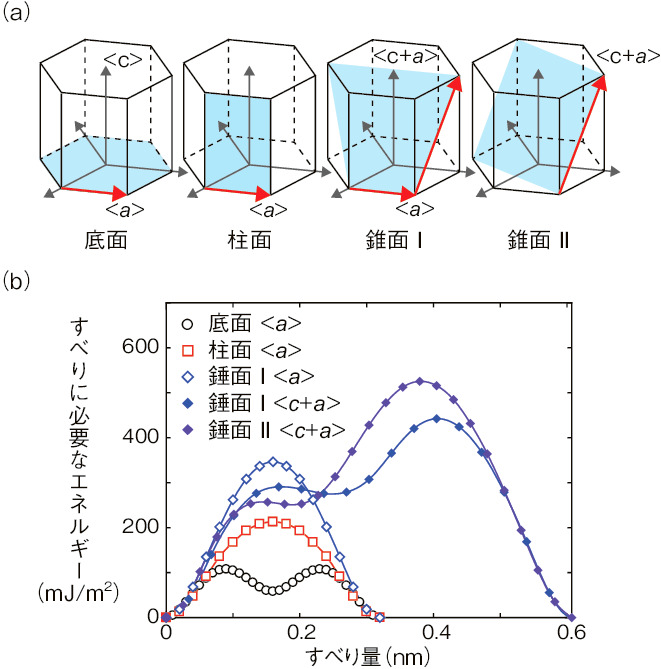
図4-15 六方晶金属のすべり面とすべりに必要なエネルギー
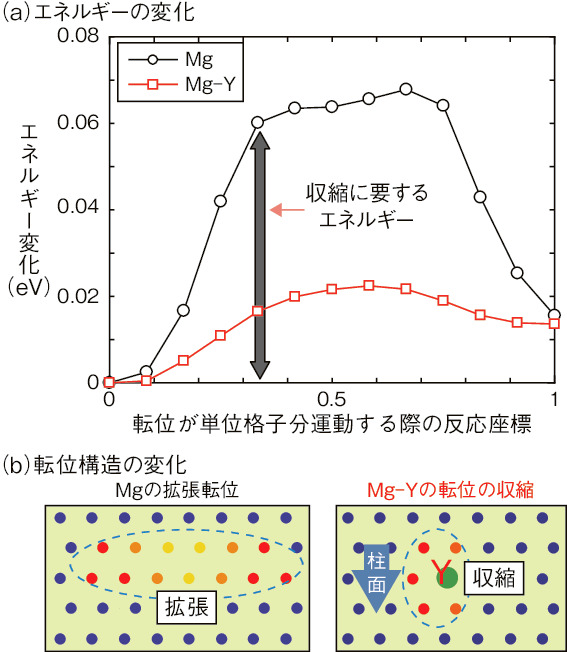
図4-16 転位運動の(a)エネルギーの変化と(b)転位構造の変化
マグネシウム(Mg)、チタン(Ti)、ジルコニウム(Zr)などの六方晶金属は、軽量、耐熱性、耐腐食特性など金属材料の中でも優れた特性を持っています。その一方で、図4-15に示すように、六方晶金属は鉄やアルミニウムなどの立方晶金属と異なり、多様な結晶面を持っており、金属材料の延性(破断せずに柔軟に変形する特性)の基礎となる転位(結晶面がすべるための欠陥)のすべり運動に大きな偏りが生じることが知られています。その結果、構造材料として用いる際に重要な加工性が悪いという致命的な欠点を併せ持っています。そのため、六方晶金属の加工性の向上にはこのような偏りをなくすことが重要になってきます。構造材料の機能向上には古くから他の元素を混ぜる合金化が用いられてきました。例えば鋼では炭素を混ぜることで固くなることが良く知られています。合金化によって金属の機械的性質は大きく変化しますが、これまで経験的な知見によってのみで模索されており、体系的に理解はされていません。
私たちは、このような合金設計に非経験的な知見を与えるため、原子・電子レベルの計算機シミュレーションによって合金化のもたらす金属材料の機械特性の変化を評価する方法に注力し、Mgを例に合金設計指針の検討を行いました。金属材料の変形は転位のすべりによって生じることから、図4-15(b)に示すようにそれぞれの結晶面のすべりに必要なエネルギーを評価しました。図から底面のエネルギーが極端に低く、底面以外のエネルギーは高くなり大きな偏りがあることが分かります。加工性の向上には底面の次に小さい柱面のエネルギーを低減して偏りを軽減する必要があります。
そこで、経験的なパラメータを排除した第一原理計算法を用いて、合金化による転位運動の高精度な解析を行いました。純Mgとイットリウム(Y)を添加したMg-Y合金中の転位運動の計算結果を図4-16に示します。図4-16(a)のエネルギー変化から、純Mgのすべりに比べて、Mg-Y合金では柱面のすべりエネルギーが大きく低減されることが分かりました。また、図4-16(b)に転位が運動する際の転位の模式図を示しています。純Mgの特徴である二つに拡張した転位は柱面を運動する際に収縮する必要があり、収縮に必要なエネルギーが大きいのに対して、Y元素は収縮した状態を安定化し、柱面上の運動が促進されることですべりの偏りが低減されることが分かりました。このように、原子レベルの解析により合金化が及ぼす機械特性の変化を計算科学によって予測できると期待されています。