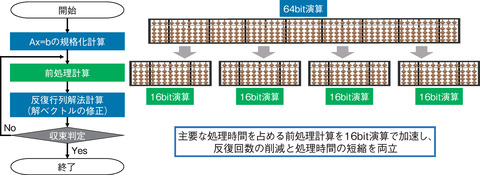
図9-4 混合精度行列解法の模式図
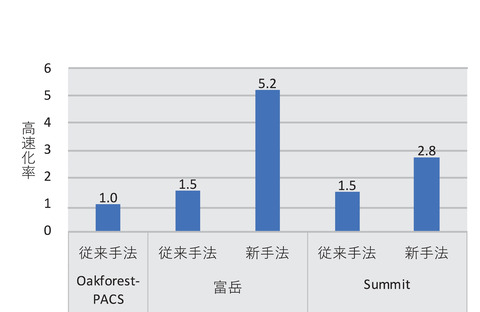
図9-5 混合精度行列解法の処理性能比較
「富岳」をはじめとする1秒間に1018回規模の演算を処理できるエクサスケール計算機を駆使した数値流体力学(CFD)解析(エクサスケール流体解析)が原子力分野を含め幅広い科学・工学分野で活用されつつあります。このような大規模CFD解析を効率的に実行するために、エクサスケール計算機向けの計算アルゴリズムが必須となっています。今回、CFD解析の中核を成す行列計算に関して、メニーコアCPU計算機「富岳」(理化学研究所)で新たに利用可能となった可変精度演算を活用した混合精度行列解法を原子力機構と理化学研究所(理研)が共同で開発しました。この解法を理研が「富岳」向け、原子力機構がGPU計算機「Summit」(オークリッジ国立研究所)向けに実装し、メニーコアCPU及びGPUに基づくエクサスケール計算機で高性能計算が可能であることを実証しました。
CFD解析では流体モデルの時間発展を離散化することで得られる連立一次方程式Ax=bを多数回計算します。ここで、格子数Nの問題に対して、CFDスキームが与える行列AはサイズN×Nの大規模疎行列、bは現在の時刻の流体変数によって決まるサイズNのベクトル、xは次の時刻の流体変数を表す解ベクトルを示します。このような大規模疎行列の計算では反復行列解法を用いますが、大規模CFD解析では1回の計算に数千回以上の反復計算が必要となっていました。反復回数を削減する方法として、前処理行列Mをかけて問題をM-1Ax=M-1bと変換して、問題を解きやすくする手法があります。ここで、MはAの近似解となるように選びますが、その近似精度は任意に選ぶことができます。本研究では前処理計算以外の反復行列解法の計算には科学技術計算で標準的な64bit演算を利用し、前処理計算に16bit演算を利用する混合精度行列解法を構築しました(図9-4)。16bit演算は機械学習で多用されており、これまでGPUでは利用可能でしたが、CPUでは「富岳」ではじめて利用可能となりました。64bit演算に比べて、16bit演算は一度に4倍の演算数を処理できるため、演算加速に有効です。本研究では、16bit演算による桁落ちを防ぐように問題を規格化することで、計算精度の劣化を回避することに成功し、反復回数を一桁削減しました。
「富岳」と「Summit」において、1440プロセッサを用いて約1000億格子規模のプラズマ流体解析を実施し、開発手法の処理性能を従来のメニーコアCPU計算機「Oakforest-PACS」(東京大学/筑波大学)と比較しました(図9-5)。ここで、CFD解析の処理性能を決める主要なハードウェア性能(メモリバンド幅)の比は「富岳」、「Summit」ともに「Oakforest-PACS」の約2倍となります。従来手法を用いた場合には1.5倍の性能向上であったのに対し、開発手法を用いた場合には「富岳」で5.2倍、「Summit」で2.8倍とハードウェア性能比を上回る性能向上が得られ、メニーコアCPUとGPUの両方で開発手法の有効性を確認できました。
本研究は、文部科学省「富岳」成果創出加速プログラム「核燃焼プラズマ閉じ込め物理の開拓(hp200127)」およびOak Ridge Leadership Computing Facility (OLCF) Director’s Discretion Project「Exascale CFD Simulations at JAEA (CSC367)」の支援の下で得られた成果です。
(井戸村 泰宏)