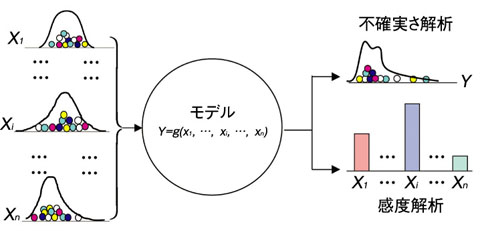
図6-13 不確実さ解析と感度解析の概念図
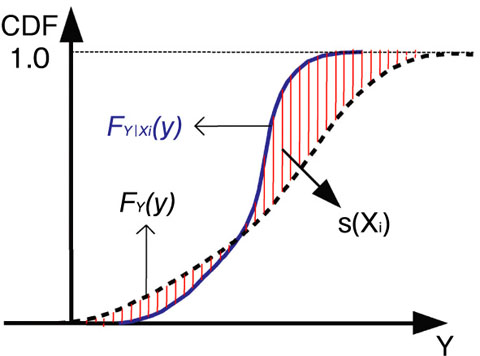
図6-14 提案した重要度指標の基本的な考え方
確率論的安全評価(PSA)は、原子力施設で起こり得る事象を対象に、炉心損傷事故等の発生頻度と公衆や社会への影響を定量的に推定し、潜在的なリスクを総合的に評価する手法です。
PSAでは、機器の故障率や人の過誤率を入力変数として原子炉の炉心損傷頻度等を評価します。これらの変数の値は不確実さを持ち、確率分布で表されます。PSAでは、入力変数の不確実さ情報を用い、モンテカルロ法で出力変数の不確実さを求めることが一般であり、以下のステップからなるプロセスで行います(図6-13)。
(1)各入力変数の確率分布に沿ってランダムに値をサンプリングし、一組の入力変数のセットを作ります。これを繰り返すことにより数千から数万個のセットを作ります。
(2)各セットの入力変数の値を用いて計算し、出力変数Y の値を求めます。
(3)得られた数千から数万個のY の値から、Y の確率分布を求めます。
一方、Yの不確実さに大きく寄与する入力変数を見いだすために、感度解析を行う必要があります(図6-13)。
従来の感度解析手法では、出力変数の不確実さを分散で表します。ある入力変数の値を固定し、他の入力変数については確率分布を与え、モンテカルロ法によって出力変数の確率分布と分散を求めます。この計算を繰り返すことにより、出力変数の分散の平均値を算出し、さらに、左記ステップ(3)で求めた確率分布、すなわち、すべての入力変数の不確実さを考慮した場合の分散との比をとり、当該入力変数の重要度と定義します。しかし、出力変数の確率分布の歪みが大きい場合には、分散では確率分布の不確実さを適切に表せません。そこで、歪みが大きい場合でも出力変数の不確実さに大きく影響する入力変数を効率的に同定できるように、新しい重要度指標を提案しました(図6-14)。この新指標は、評価結果の確率分布の形がどの程度変化するかを定量的に評価し、その大きさを入力変数の重要度と定義します。新指標は、従来の手法と比べて、分布の形に依存しないという特徴があります。
さらに、提案した新重要度指標を組み込み、PSAにおける不確実さ及び感度解析を行えるコードGSALab(Global Sensitivity Analysis Lab)を開発しました。同コードの開発により、より精度の高いPSAの結果を得ることが可能となりました。また、GSALabは、原子力施設のPSAに限らず、大気拡散モデルなど、様々なモデルの不確実さ・感度解析にも適用可能な汎用コードです。