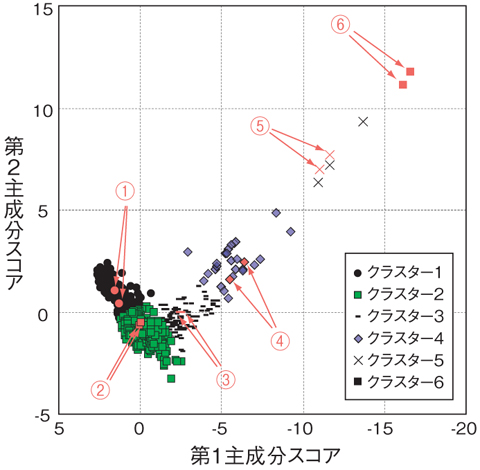
図3-15 第1及び第2主成分の散布図及びクラスタリングの結果

図3-16 各クラスターに対応するボーリングコア
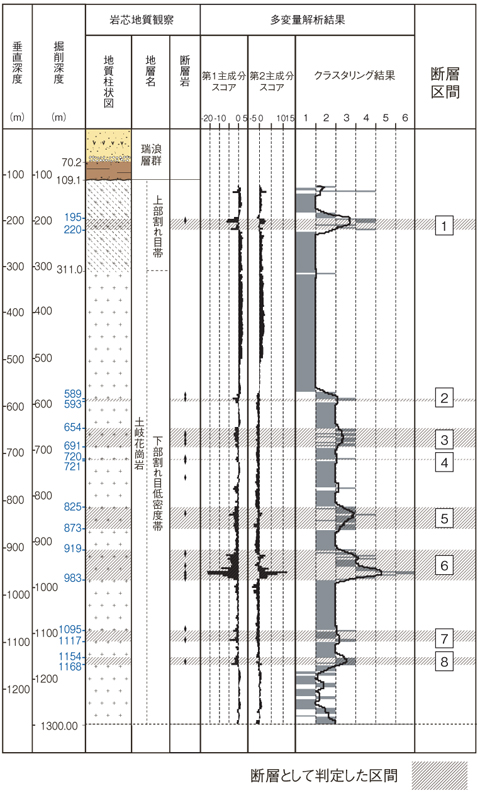
図3-17 ボーリング孔における断層区間
断層は、その形成に伴う岩盤の変形や変質等により、岩盤の物性や透水性等に影響を及ぼします。そのため、地下空間の利用にあたっては、断層の影響を受けた部分(この説明では、断層区間と呼びます)の特定は重要な課題です。しかし、断層を対象とした調査では、取得できる情報の種類、量やその品質にばらつきがあることに加え、調査を担当する技術者の熟練度や知識量によって、断層区間の判定結果が異なる可能性があります。そこで、私たちは客観的な基準によって断層区間の特定方法を検討するため、瑞浪超深地層研究所(以下、研究所)におけるボーリング調査で取得したデータを用いた数値解析を行いました。
検討対象のボーリング孔は、研究所で実施した掘削長1300 mのボーリング孔で、いくつかの深度に断層が存在することが確認されていました。このボーリング調査では、コアの地質観察のほか、ほぼ全深度にわたって物理検層を実施しており、定量的な数値データが取得されています。物理検層の中で岩盤の変形などによって数値が大きく変動する項目に着目し、それらのデータ間の関連性を同時に解析することが可能な主成分分析を行い、データの分散が大きい(元データの情報が多く保存されているため、数値の分布範囲が広い)第1及び第2成分の散布図を作成しました。更に散布図の区分を行うため、区分の良さの評価関数によって区分の最適解を求めるk-means法というクラスタリングを実施しました(図3- 15)。図3- 16にそれぞれのクラスターに対応するボーリングコアを示します。岩盤の状態が悪いほど図3- 15の右側にプロットされていることが分かります。図3- 16に示すコアの地質観察から、クラスター3〜6が断層区間に相当することから、ボーリング孔の全深度について、クラスター3〜6に相当する区間を抽出し、合計で8区間の断層区間を判定することができました(図3- 17)。この断層区間については、ボーリングコアの地質観察やほかのデータの検討からも断層区間と判定されており、この手法で適切に断層区間が判定されていることが確かめられています。この手法は調査量や技術者の熟練度などに左右されない客観性と追跡性を有していることから、信頼性の高い地下空間の調査・評価手法に大きく寄与すると考えています。
本研究は、日本情報地質学会の2011年度「論文賞」に選ばれました。